HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Wednesday, July 27, 2022

AP Board Class 8 Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions PDF: Download Andhra Pradesh Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Book Answers

            No comments    
AP Board Class 8 Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions PDF: Download Andhra Pradesh Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Book Answers
AP Board Class 8 Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions PDF: Download Andhra Pradesh Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Book Answers


AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 book solutions pdf online from this page.

Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks Solutions PDF

Andhra Pradesh State Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks. These Andhra Pradesh State Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Books Solutions

Board AP Board
Materials Textbook Solutions/Guide
Format DOC/PDF
Class 8th
Subject Maths
Chapters Maths Chapter 12 Factorisation Ex 12.2
Provider Hsslive


How to download Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions Answers PDF Online?

  1. Visit our website - Hsslive
  2. Click on the Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Answers.
  3. Look for your Andhra Pradesh Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks PDF.
  4. Now download or read the Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions for PDF Free.


AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

Question 1.
Factorise the following expression
i) a2 + 10a +25
ii) l2 – 16l + 64
iii) 36x2 + 96xy + 64y2
iv) 25x2 + 9y2 – 30xy
v) 25m2– 40mn + 1 6n2
vi) 81x2 – 198 xy + 12ly2
vii) (x+y)2 – 4xy
(Hint : first expand ( x + y)2 )
viii) l4 + 4l2m2 + 4m4
Solution:
i) a2 + 10a +25
= (a)2 + 2 × a × 5 + (5)2
It is in the form of a2 + 2ab + b2
a2 + 2ab + b2= (a + b)2
∴ a2 + 10a + 25 = (a + 5)2 = (a + 5) (a + 5)

ii) l2 – 16l + 64
l2 – 16l + 64
= (l)2 – 2 × l × 8 + (8)2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ l2 – 16l + 64 = (l – 8)2 = (l – 8) (l – 8)

iii) 36x2 + 96xy + 64y2
36x2 + 96xy + 64y2
= (6x)2 + 2 × 6x × 8y + (8y)2
It is in the form of a2 + 2ab + b2
a2 + 2ab + b2 = (a + b)2
∴ 36x2 + 96xy + 64y2
= (6x + 8y)2 = (6x + 8y) (6x + 8y)

iv) 25x2 + 9y2 – 30xy
25x2 + 9y2 – 30xy
= (5x)2 + (3y)2 – 2 × 5x × 3y
It is in the form of a2 + b2 – 2ab
a2 + b2 – 2ab = (a – b)2
∴ 25x2 + 9y2 – 30xy
= (5x – 3y)2 = (5x – 3y) (5x – 3y)

v) 25m2– 40mn + 1 6n2
25m2 – 40mn + 16n2
= (5m)2 – 2 × 5m × 4n + (4n)2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ 25m2 – 40mn + 16n2
= (5m – 4n)2
= (5m – 4n) (5m – 4n)

vi) 81x2 – 198 xy + 12ly2
81x2 – 198xy + 121y2
= (9x)2 – 2 × 9x × 11y + (11y)2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ 81x2 – 198xy + 121y2
= (9x – 11y)2 – (9x – 11y) (9x – 11y)

vii) (x+y)2 – 4xy
(Hint : first expand ( x + y)2 )
= (x + y)2 – 4xy
= x2 + y2 + 2xy – 4xy
= x2 + y2 – 2xy = (x – y)2 = (x – y)(x – y)

viii) l4 + 4l2m2 + 4m4
l4 + 4l2m2 + 4m4
= (l2)2 + 2 × l2 × 2m2 + (2m2)2
It is in the form of a2 + 2ab + b2
a2 + 2ab + b2 = (a – b)2
∴ l4 + 4l2m2 + 4m4
= (l2 + 2m2)2 = (l2 + 2m2) (l2 + 2m2)

Question 2.
Factorise the following
i) x2 – 36
ii) 49x2 – 25y2
iii) m2 – 121
iv) 81 – 64x2
v) x2y2 – 64
vi) 6x2 – 54
vii) x2 – 81
viii) 2x -32 x5
ix) 81x4 – 121x2
x) (p2 – 2pq + q2)-r2
xi) (x+y)2 – (x-y)2
Solution:
i) x2 – 36
x2 – 36
⇒ (x)2 – (6)2 is in the form of a2 – b2
a2 – b2 = (a + b) (a – b)
∴ x2 – 36 = (x + 6) (x – 6)

ii) 49x2 – 25y2
= (7x)2 – (5y)2
= (7x + 5y) (7x – 5y)

iii) m2 – 121
m2 -121
= (m)2 – (11)2
= (m + 11) (m – 11)

iv) 81 – 64x2
81 – 64x2
= (9)2 – (8x)2
= (9 + 8x) (9 – 8x)

v) x2y2 – 64
= (xy)2 – (8)2
= (xy + 8)(xy – 8)

vi) 6x2 – 54
6x2 – 54
= 6x2 – 6 x 9 ‘
= 6(x2 – 9)
= 6[(x)2 – (3)2]
= 6(x + 3) (x – 3)

vii) x2 – 81
x2 – 81
= x2 – 92
= (x + 9 )(x – 9)

viii) 2x – 32 x5
2x – 32 x5
= 2x – 2x x 16x4
= 2 x (1 – 16x4)
= 2x [12) – (4x2)2]
= 2x (1 + 4x2) (1 – 4x2)
= 2x (1 + 4x2) [(15 – (2x)2]
= 2x (1 + 4x2) (1 + 2x) (1 – 2x)

ix) 81x4 – 121x2
81x4 – 121x2
– x2 (812 – 121)
= x2[(9x)2 – (11)2]
= x2 (9x + 11) (9x -11)

x) (p2 – 2pq + q2)-r2
(p2 – 2pq + q2) – r2
= (p – q)2 – (r)2 [∵ p2 – 2pq + q2 = (p – q)2]
= (p – q + r) (p – q – r)

xi) (x + y)2 – (x – y)2
(x + y)2 – (x – y)2
It is in the form of a2 – b2
a = x + y, b = x- y
∴ a2 – b2 =(a + b)(a-b)
= (x + y + x – y) [x + y- (x – y)]
= 2x [x + y-x + y]
= 2x x 2y = 4xy

Question 3.
Factorise the expressions
(i) lx2 + mx
(ii) 7y2 + 35Z2
(iii) 3x4 + 6x3y + 9x2Z
(iv) x2 – ax – bx + ab
(v) 3ax – 6ay – 8by + 4bx
(vi) mn + m + n + 1
(vii) 6ab – b2 + 12ac – 2bc
(viii) p2q – pr2 – pq + r2
(ix) x (y + z) -5 (y + z)

(i) lx2 + mx
lx2 + mx
= l × x × x + m × x = x(lx + m)

(ii) 7y2 + 35z2
7y2+ 35z2
= 7 × y2 + 7 × 5 × z2
= 7(y2 + 5z2)

(iii) 3x4 + 6x3y + 9x2Z
3x4 + 6x3y + 9x2Z
= 3 × x2 × x2 + 3 × 2 × x × x2 × y + 3 × 3 × x2 × z
= 3x2 (x2 + 2xy + 3z)

(iv) x2 – ax – bx + ab
x2 – ax – bx + ab
= (x2 – ax) – (bx – ab)
= x(x – a) – b(x – a)
= (x – a) (x – b)

(v) 3ax – 6ay – 8by + 4bx
3ax – 6ay – 8by + 4bx
= (3ax – 6ay) + (4bx – 8by)
= 3a (x – 2y) + 4b (x – 2y)
= (x – 2y) (3a + 4b)

(vi) mn + m + n + 1
mn + m + n + 1
= (mn + m) + (n + 1)
= m (n + 1) + (n + 1)
= (n + 1) (m + 1)

(vii) 6ab – b2 + 12ac – 2bc
6ab – b2 + 12ac – 2bc
= (6ab – b2) + (12ac – 2bc)
= (6 × a× b – b × b) + (6 × 2 × a × c – 2 × b × c)
= b [6a – b] + 2c [6a – b]
= (6a – b) (b + 2c)

(viii) p2q – pr2 – pq + r2
p2q – pr2 – pq + r2
= (p2q – pr2) – (pq – r2)
= (p × p × q – p × r × r) – (pq – r2)
= P(pq – r2) – (pq – r2) × 1
= (pq – r2)(p – 1)

(ix) x (y + z) -5 (y + z)
= x(y + z) – 5(y + z)
= (y + z) (x – 5)

Question 4.
Factorise the following
(i) x4 – y4
(ii) a4 – (b + c)4
(iii) l2 – (m – n)2
(iv) 49x2 – 1625
(v) x4 – 2x2y2 + y4
(vi) 4 (a + b)2 – 9 (a – b)2
Solution:
= (x2)2 – (y2)2 is in the form of a2 – b2
a2 – b2 = (a + b) (a – b)
x4 – y4 = (x2 + y2)(x2 – y2)
= (x2 + y2)(x + y)(x – y)

(ii) a4 – (b + c)4
a4 – (b + c)4
= (a2)2 – [(b + c)2]2
= [a2 + (b + c)2] [a2 – (b + c)2] ,
= [a2 + (b + c)2] (a + b + c) [a – (b + c)]
= [a2 + (b + c)2] (a + b + c) (a – b – c)

(iii) l2 – (m – n)2
l2 – (m – n)2
= (l)2 – (m – n)2
= [l + m – n] [l – (m – n)]
= [l + m -n] [l – m + n]

(iv) 49x2 – 1625
= (7x)2 – (45)2
= (7x+ (45) (7x – (45)

(v) x4 – 2x2 y2 + y4
= (x2 )2 – 2x2 y2 + (y2 )2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ x4 – 2x2 y2 + y4 = (x2 – y2 )2
= [(x)2 – (y)2 ]2
= [(x + y) (x – y)]2
= (x + y)2 (x – y)2
[∵ (ab)m = a m . bn ]

(vi) 4 (a + b)2 – 9 (a – b)2
4 (a + b)2 – 9 (a – b)2
= [2(a + b)]2 – [3(a – b)]2
= [2(a + b) + 3(a- b)] [2(a + b)-3(a- b)]
= (2a + 2b + 3a – 3b) (2a + 2b – 3a + 3b)
= (5a – b) (5b – a)

Question 5.
Factorise the following expressions
(i) a2+ 10a + 24
(ii) x2 +9x + 18
(iii) p2 – 10q + 21
(iv) x2 – 4x – 32
Solution:
(i) a2+ 10a + 24
a2 + 10a + 24 .
= a2 + 6a + 4a + 24
= a x a + 6a + 4a + 6 × 4
= a(a + 6) + 4(a + 6)
= (a + 6) (a + 4) (or)
a2 + 10a + 24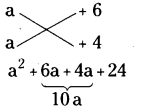

∴ a2 + 10a + 24 = (a + 6) (a + 4)

(ii) x2 + 9x + 18
x2 + 9x + 18
= (x + 3) (x + 6)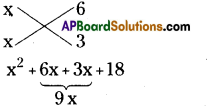

∴ x2 + 9x + 18 = (x + 3) (x + 6)

(iii) p2 – 10q + 21
p2 – 10p + 21
= (P – 7) (p – 3)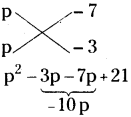

∴ p2 – 10p + 21 = (p – 7)(p – 3)

(iv) x2 – 4x – 32
x2 – 4x – 32
= (x – 8) (x + 4)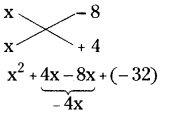

∴ x2 – 4x – 32 = (x – 8) (x + 4)

Question 6.
The lengths of the sides of a triangle are integrals, and its area is also integer. One side is 21 and the perimeter is 48. Find the shortest side.
Solution:
Perimeter of a triangle
= AB + BC + CA = 48
⇒ c + a + b = 48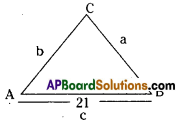

The solutions of Harmeet, Rosy are wrong.

∴ Srikar had done it correctly.
⇒ 21 + a + b = 48
⇒ a + b = 48 – 21 = 27
∴ The lengths of a, b should be 10, 17
∴ a + b > c [the sum of any two sides of a triangle is greater than the 3rd side]
∴ 10 + 17 > 2
27 > 21 (T).
∴ The length of the shortest side is 10 cm.

Question 7.
Find the values of ‘m’ for which x2 + 3xy + x + my – in has two linear factors in x and y, with integer coefficients.
Solution:
Given equation is x2 + 3xy + x + my – m ……….(1)
Let the two linear equations in x and y be (x + 3y + a) and (x + 0y + b).
Then (x + 3y + a) (x + 0y + b)
= x2 + 0xy + bx + 3xy + 0y2 + 3by + ax + 0y + ab
= x2 + bx + ax + 3xy + 3by + ab ………….. (2)
Comparing equation (2) with (1),
x2 + 3xy + x + my – m
= x2 + (a + b)x + 3xy + 3by + ab
Equating the like terms on both sides,
ab = – m ………….. (3)
(a + b)x = x ⇒ a + b = 1 ……………. (4)
3by = my ⇒ 3b = m ⇒ b = m3
Substitute ‘b’ value in equation (4),
a = 1−𝑚3=3−𝑚3
ab = -m
[ ∵ from (3)]
put a & b value then ,
(3−𝑚3)(𝑚3) = -m
3 m−m29= -m
⇒ 3m – m2 = – 9m
⇒ m2 – 12m = 0
⇒ m(m – 12) = 0
⇒ m = 0 (or) m = 12
lf m = 12

∴ b = 123 = 4&a = 3−m3=3−123
= −93 = -3
∴ Linear factors are (x + 3y – 3), (x + 4) If m = 0
b = 03 = 0 & a = 3−03=33 = 1
∴ Linear factors are (x + 3y + 1), x.


AP Board Textbook Solutions PDF for Class 8th Maths


Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks for Exam Preparations

Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 exam preparation. The AP Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 8th Maths Chapter 12 Factorisation Ex 12.2 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook Solutions


How to get AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook Answers??

Students can download the Andhra Pradesh Board Class 8 Maths Chapter 12 Factorisation Ex 12.2 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 8th Maths Chapter 12 Factorisation Ex 12.2, AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks, Andhra Pradesh State Board Class 8th Maths Chapter 12 Factorisation Ex 12.2, Andhra Pradesh State Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook solutions, AP Board Class 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks Solutions, Andhra Pradesh Board STD 8th Maths Chapter 12 Factorisation Ex 12.2, AP Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks, Andhra Pradesh State Board STD 8th Maths Chapter 12 Factorisation Ex 12.2, Andhra Pradesh State Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Textbook solutions, AP Board STD 8th Maths Chapter 12 Factorisation Ex 12.2 Textbooks Solutions,
Share:

0 Comments:

Post a Comment

Plus Two (+2) Previous Year Question Papers

Plus Two (+2) Previous Year Chapter Wise Question Papers, Plus Two (+2) Physics Previous Year Chapter Wise Question Papers , Plus Two (+2) Chemistry Previous Year Chapter Wise Question Papers, Plus Two (+2) Maths Previous Year Chapter Wise Question Papers, Plus Two (+2) Zoology Previous Year Chapter Wise Question Papers, Plus Two (+2) Botany Previous Year Chapter Wise Question Papers, Plus Two (+2) Computer Science Previous Year Chapter Wise Question Papers, Plus Two (+2) Computer Application Previous Year Chapter Wise Question Papers, Plus Two (+2) Commerce Previous Year Chapter Wise Question Papers , Plus Two (+2) Humanities Previous Year Chapter Wise Question Papers , Plus Two (+2) Economics Previous Year Chapter Wise Question Papers , Plus Two (+2) History Previous Year Chapter Wise Question Papers , Plus Two (+2) Islamic History Previous Year Chapter Wise Question Papers, Plus Two (+2) Psychology Previous Year Chapter Wise Question Papers , Plus Two (+2) Sociology Previous Year Chapter Wise Question Papers , Plus Two (+2) Political Science Previous Year Chapter Wise Question Papers, Plus Two (+2) Geography Previous Year Chapter Wise Question Papers, Plus Two (+2) Accountancy Previous Year Chapter Wise Question Papers, Plus Two (+2) Business Studies Previous Year Chapter Wise Question Papers, Plus Two (+2) English Previous Year Chapter Wise Question Papers , Plus Two (+2) Hindi Previous Year Chapter Wise Question Papers, Plus Two (+2) Arabic Previous Year Chapter Wise Question Papers, Plus Two (+2) Kaithang Previous Year Chapter Wise Question Papers , Plus Two (+2) Malayalam Previous Year Chapter Wise Question Papers

Plus One (+1) Previous Year Question Papers

Plus One (+1) Previous Year Chapter Wise Question Papers, Plus One (+1) Physics Previous Year Chapter Wise Question Papers , Plus One (+1) Chemistry Previous Year Chapter Wise Question Papers, Plus One (+1) Maths Previous Year Chapter Wise Question Papers, Plus One (+1) Zoology Previous Year Chapter Wise Question Papers , Plus One (+1) Botany Previous Year Chapter Wise Question Papers, Plus One (+1) Computer Science Previous Year Chapter Wise Question Papers, Plus One (+1) Computer Application Previous Year Chapter Wise Question Papers, Plus One (+1) Commerce Previous Year Chapter Wise Question Papers , Plus One (+1) Humanities Previous Year Chapter Wise Question Papers , Plus One (+1) Economics Previous Year Chapter Wise Question Papers , Plus One (+1) History Previous Year Chapter Wise Question Papers , Plus One (+1) Islamic History Previous Year Chapter Wise Question Papers, Plus One (+1) Psychology Previous Year Chapter Wise Question Papers , Plus One (+1) Sociology Previous Year Chapter Wise Question Papers , Plus One (+1) Political Science Previous Year Chapter Wise Question Papers, Plus One (+1) Geography Previous Year Chapter Wise Question Papers , Plus One (+1) Accountancy Previous Year Chapter Wise Question Papers, Plus One (+1) Business Studies Previous Year Chapter Wise Question Papers, Plus One (+1) English Previous Year Chapter Wise Question Papers , Plus One (+1) Hindi Previous Year Chapter Wise Question Papers, Plus One (+1) Arabic Previous Year Chapter Wise Question Papers, Plus One (+1) Kaithang Previous Year Chapter Wise Question Papers , Plus One (+1) Malayalam Previous Year Chapter Wise Question Papers

Resource

Copyright © HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board About | Contact | Privacy Policy