AP Board Class 9 Maths Chapter 12 Circles Ex 12.4 Textbook Solutions PDF: Download Andhra Pradesh Board STD 9th Maths Chapter 12 Circles Ex 12.4 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

AP Board Class 9 Maths Chapter 12 Circles Ex 12.4 Textbook Solutions PDF: Download Andhra Pradesh Board STD 9th Maths Chapter 12 Circles Ex 12.4 Book Answers

AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 9th Maths Chapter 12 Circles Ex 12.4 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 9th Maths Chapter 12 Circles Ex 12.4 book solutions pdf online from this page.

Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks Solutions PDF

Andhra Pradesh State Board STD 9th Maths Chapter 12 Circles Ex 12.4 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 9th Maths Chapter 12 Circles Ex 12.4 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 9th Maths Chapter 12 Circles Ex 12.4 Textbooks. These Andhra Pradesh State Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 9th Maths Chapter 12 Circles Ex 12.4 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	9th
Subject	Maths
Chapters	Maths Chapter 12 Circles Ex 12.4
Provider	Hsslive

How to download Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Answers.
Look for your Andhra Pradesh Board STD 9th Maths Chapter 12 Circles Ex 12.4 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook Solutions for PDF Free.

AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.4

Question 1.
In the figure, ‘O’ is the centre of the circle. ∠AOB = 100°, find ∠ADB.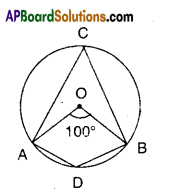

Solution:
’O’ is the centre
∠AOB = 100°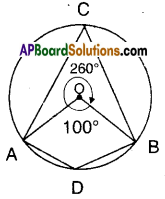

Thus ∠ACB = 12 ∠AOB
[∵ angle made by an arc at the centre is twice the angle made by it on the remaining part]]
= 12 x 100° = 50°
∠ACB and ∠ADB are supplementary
[ ∵ Opp. angles of a cyclic quadrilateral]
∴ ∠ADB = 180°-50° = 130°
[OR]
∠ADB is the angle made by the major arc ACBˆ at D.
∴ ∠ADB = 12∠AOB [where ∠AOB is the angle; made by ACBˆ at the centre]
= 12 [360° – 100°] [from the figure]
= 12 x 260° = 130°

Question 2.
In the figure, ∠BAD = 40° then find ∠BCD.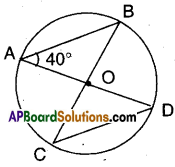

Solution:
‘O’ is the centre of the circle.
∴ In ΔOAB; OA = OB (radii)
∴ ∠OAB = ∠OBA = 40°
(∵ angles opp. to equal sides)
Now ∠AOB = 180° – (40° + 40°)
(∵ angle sum property of ΔOAB)
= 180°-80° = 100°
But ∠AOB = ∠COD = 100°
Also ∠OCD = ∠ODC [OC = OD]
= 40° as in ΔOAB
∴ ∠BCD = 40°
(OR)
In ΔOAB and ΔOCD
OA = OD (radii)
OB = OC (radii)
∠AOB = ∠COD (vertically opp. angles)
∴ ΔOAB ≅ ΔOCD
∴ ∠BCD = ∠OBA = 40°
[ ∵ OB = OA ⇒ ∠DAB = ∠DBA]

Question 3.
In the figure, ‘O’ is the centre of the circle and ∠POR = 120°. Find ∠PQR and ∠PSR.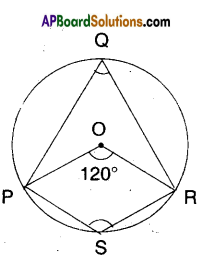

Solution:
‘O’ is the centre; ∠POR = 120°
∠PQR = 12∠POR [∵ angle made by an arc at the centre is, twice the angle made by it on the remaining part]
∠PSR = 12 [Angle made by PQRˆ at the centre]
∠PSR = 12 [360° – 120°] from the fig.
= 12 x 240 = 120°

Question 4.
If a parallelogram is cyclic, then it is a rectangle. Justify.
Solution: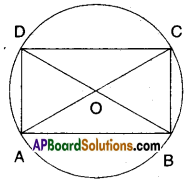

Let □ABCD be a parallelogram such
that A, B, C and D lie on the circle.
∴∠A + ∠C = 180° and ∠B + ∠D = 180°
[Opp. angles of a cyclic quadri lateral are supplementary]
But ∠A = ∠C and ∠B = ∠D
[∵ Opp. angles of a ||gm are equal]
∴∠A = ∠C =∠B =∠D = 1802 = 90°
Hence □ABCD is a rectangle

Question 5.
In the figure, ‘O’ is the centr of the circle. 0M = 3 cm and AB = 8 cm. Find the radius of the circle.

Solution: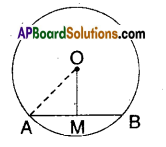

‘O’ is the centre of the circle.
OM bisects AB.
∴ AM = AB2=82 = 4 cm
OA² = OM² + AM² [ ∵ Pythagoras theorem]
OA =32+42‾‾‾‾‾‾‾√=9+16‾‾‾‾‾‾√=25‾‾‾√
= 5cm

Question 6.
In the figure, ‘O’ is the centre of the circle and OM, ON are the perpen-diculars from the centre to the chords PQ and RS. If OM = ON and PQ = 6 cm. Find RS.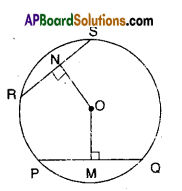

Solution:
‘O’ is the centre of the circle.
OM = ON and 0M ⊥ PQ; ON ⊥ RS
Thus the chords FQ and RS are equal.
[ ∵ chords which are equidistant from the centre are equal in length]
∴ RS = PQ = 6cm

Question 7.
A is the centre of the circle and ABCD is a square. If BD = 4 cm then find the
radius of the circle.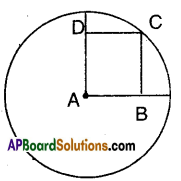

Solution: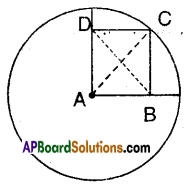

A is the centre of the circle and ABCD is a square, then AC and BD are its diagonals. Also AC = BD = 4 cm But AC is the radius of the circle.
∴ Radius = 4 cm.

Question 8.
Draw a circle with any radius and then draw two chords equidistant
from the centre.
Solution: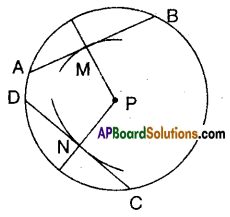

Draw a circle with centre P.
Draw any two radii.
Mark off two points M and N oh these radii. Such that PM = PN.
Draw perpendicular through M and N to these radii.

Question 9.
In the given figure, ‘O’ is the centre of the circle and AB, CD are equal chords. If ∠AOB = 70°. Find the angles of ΔOCD.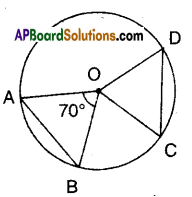

Solution:
‘O’ is the centre of the circle.
AB, CD are equal chords
⇒ They subtend equal angles at the centre.
∴ ∠AOB =∠COD = 70°
Now in ΔOCD
∠OCD = ∠ODC [∵ OC = OD; radii angles opp. to equal sides]
∴ ∠OCD + ∠ODC + 70° = 180°
= ∠OCD +∠ODC = 180° – 70° = 110°
∴ ∠OCD + ∠ODC = 110° = 55°

AP Board Textbook Solutions PDF for Class 9th Telugu

Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks for Exam Preparations

Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 exam preparation. The AP Board STD 9th Maths Chapter 12 Circles Ex 12.4 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 9th Maths Chapter 12 Circles Ex 12.4 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook Solutions

How to get AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook Answers??

Students can download the Andhra Pradesh Board Class 9 Maths Chapter 12 Circles Ex 12.4 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 9th Maths Chapter 12 Circles Ex 12.4, AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks, Andhra Pradesh State Board Class 9th Maths Chapter 12 Circles Ex 12.4, Andhra Pradesh State Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbook solutions, AP Board Class 9th Maths Chapter 12 Circles Ex 12.4 Textbooks Solutions, Andhra Pradesh Board STD 9th Maths Chapter 12 Circles Ex 12.4, AP Board STD 9th Maths Chapter 12 Circles Ex 12.4 Textbooks, Andhra Pradesh State Board STD 9th Maths Chapter 12 Circles Ex 12.4, Andhra Pradesh State Board STD 9th Maths Chapter 12 Circles Ex 12.4 Textbook solutions, AP Board STD 9th Maths Chapter 12 Circles Ex 12.4 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, July 14, 2022