 |
| AP Board Class 9 Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Book Answers |
Andhra Pradesh Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbooks Solutions PDF
Andhra Pradesh State Board STD 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbooks. These Andhra Pradesh State Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 9th |
| Subject | Maths |
| Chapters | Maths Chapter 13 Geometrical Constructions Ex 13.1 |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Answers.
- Look for your Andhra Pradesh Board STD 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbook Solutions for PDF Free.
AP Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 9th Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions Exercise 13.1
Question 1.
Construct the following angles at the initial point of a given ray and justify the construction.
a) 90°
Solution: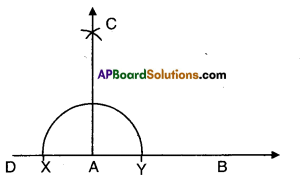
- Let AB be the given ray.
- Produce BA to D.
- Taking A as centre draw a semi circle with some radius.
- With X and Y as Center draw two intersecting arcs of same radius.
Or
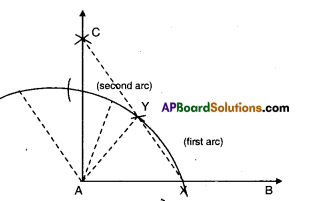 |
|
- Let AB−→− be the given ray.
- With A as centre draw an arc of any radius.
- Mark off two equal arcs from X as shown in the figure with the same radius taken as before.
- Bisect the second segment.
- Join the point of intersection of above arcs, with A.
- ∠BAC is the required right angle.
- Join the point of intersection ‘C’ and ‘A’.
- ∠BAC = 90°
In ΔAXY; ∠YAX = 60° and
in ΔAYC ∠YAC = 30° ∠BAC = 90°
b) 45°
Solution:
Steps:
- Construct 90° with the given ray AB.
- Bisect it from ∠BAD = 45°
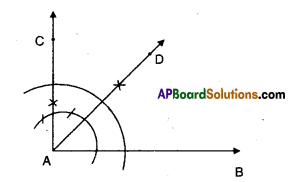
Or
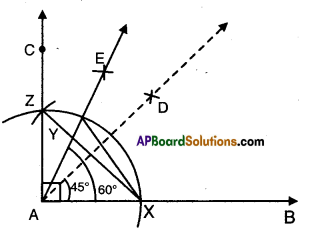
Steps:
- Construct ∠BAC = 60°
- Bisect ∠BAC = ∠DAC = 30°
- Bisect ∠DAC such that ∠DAE = ∠FAC = 15°
- ∠BAE=45°
ΔAXZ is equilateral
and ∠YAZ = 15°
∴∠XAY = 45°
Question 2.
Construct the following angles using ruler and compass and verify by measuring them by a protractor.
a) 30°
Solution: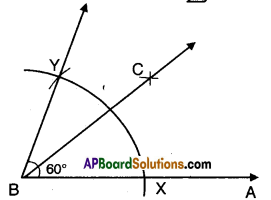
- Construct ∠ABY = 60°
- Bisect ∠ABY = 60°
- Such that ∠ABC = ∠CBY = 30°
b) 2212∘
Solution: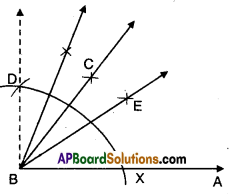
- Construct ∠ABD = 90°.
- Bisect ∠ABD such that ∠ABC = ∠CBD = 45°
- Bisect ∠ABC such that
∠ABE = ∠EBC = 2212∘
c) 15°
Solution: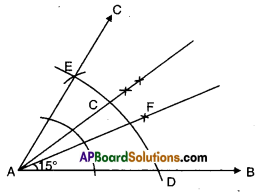
Steps of construction : ,
- Construct ∠BAE = 60°
- Bisect ∠BAE such that ∠BAC = ∠CAE = 30°
- Bisect ∠BAC such that ∠BAF = ∠FAC = 15°
d) 75°
Solution: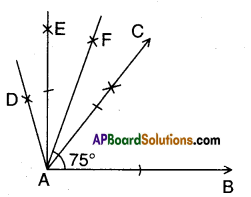
Steps of construction :
- Construct ∠BAC = 60°
- Construct ∠CAD = 60°
- Bisect ∠CAD such that ∠BAE = 90°
- Bisect ∠CAE such that ∠BAF = 75°
e) 105°
Solution: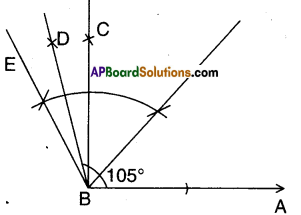
Steps of construction:
- Construct ∠ABC = 90°
- Construct ∠CBE = 30°
- Bisect ∠CBE such that the angle formed ∠ABD = 105°
f) 135°
Solution: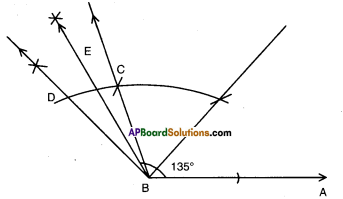
Steps of construction:
- Construct ∠ABC = 120°
- Construct ∠CBD = 30°
- Bisect ∠CBD such that the angle formed ∠ABE = 135°
Question 3.
Construct an equilateral triangle, given its side of length of 4.5 cm and justify the constraction.
Solution:
A.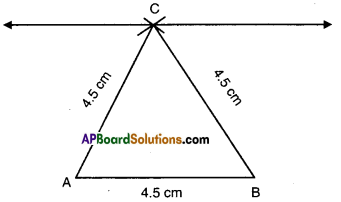
- Draw a line segment AB = 4.5 cm.
- With B and A as centres draw two arcs of radius 4.5 cm meeting at C.
- Join C to A and B.
- ΔABC is the required triangle.
Justification:
In ΔABC
AB = ∠C ⇒ ∠C = ∠B
Also AB = BC ⇒ ∠C = ∠A
Hence ∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
∴ ∠A = ∠B = ∠C = 180∘3 = 60°
Question 4.
Construct an isosceles triangle, given its base and base angle and justify the construction. [Hint: You can take any measure of side and angle]
Solution:
A.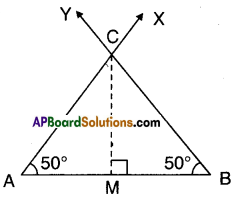
Steps:
- Draw a line segment AB of any given length.
- Construct ∠BAX and ∠ABY at A and B such that ∠A = ∠B.
- AX−→− and BY−→− will intersect at C.
- ΔABC is the required triangle.
Justification:
Drop a perpendicular CM to AB from C.
Now in ΔAMC and ΔBMC
∠AMC = ∠BMC [Right angle]
∠A = ∠B [Construction]
CM = CM (Common)
∴ ΔAMC ≅ ΔBMC
⇒ AC = BC [CPCT]
AP Board Textbook Solutions PDF for Class 9th Telugu
- AP Board Class 9 Textbook Solutions PDF
- AP Board Class 9 Maths Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 Polynomials and Factorisation Ex 2.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 Polynomials and Factorisation Ex 2.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 Polynomials and Factorisation Ex 2.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 Polynomials and Factorisation Ex 2.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 Polynomials and Factorisation Ex 2.5 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 Polynomials and Factorisation InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 3 The Elements of Geometry Ex 3.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 3 The Elements of Geometry InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 Lines and Angles Ex 4.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 Lines and Angles Ex 4.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 Lines and Angles Ex 4.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 Lines and Angles Ex 4.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 Lines and Angles InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 Co-Ordinate Geometry Ex 5.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 Co-Ordinate Geometry Ex 5.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 Co-Ordinate Geometry Ex 5.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 Co-Ordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 Linear Equation in Two Variables Ex 6.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 Linear Equation in Two Variables Ex 6.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 Linear Equation in Two Variables Ex 6.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 Linear Equation in Two Variables Ex 6.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 Linear Equation in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 Triangles Ex 7.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 Triangles Ex 7.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 Triangles Ex 7.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 Triangles InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 Quadrilaterals Ex 8.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 Quadrilaterals Ex 8.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 Quadrilaterals Ex 8.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 Quadrilaterals Ex 8.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 Quadrilaterals InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 9 Statistics Ex 9.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 9 Statistics Ex 9.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 9 Statistics InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 Surface Areas and Volumes Ex 10.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 Surface Areas and Volumes Ex 10.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 Surface Areas and Volumes Ex 10.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 Surface Areas and Volumes Ex 10.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 Surface Areas and Volumes InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 Areas Ex 11.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 Areas Ex 11.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 Areas Ex 11.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 Areas InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 Circles Ex 12.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 Circles Ex 12.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 Circles Ex 12.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 Circles Ex 12.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 Circles Ex 12.5 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 Circles InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 13 Geometrical Constructions Ex 13.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 13 Geometrical Constructions Ex 13.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 13 Geometrical Constructions InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 14 Probability Ex 14.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 14 Probability InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 Proofs in Mathematics Ex 15.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 Proofs in Mathematics Ex 15.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 Proofs in Mathematics Ex 15.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 Proofs in Mathematics Ex 15.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 Proofs in Mathematics InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 వాస్తవ సంఖ్యలు Ex 1.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 వాస్తవ సంఖ్యలు Ex 1.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 వాస్తవ సంఖ్యలు Ex 1.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 వాస్తవ సంఖ్యలు Ex 1.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 1 వాస్తవ సంఖ్యలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 బహుపదులు మరియు కారణాంక విభజన Ex 2.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 బహుపదులు మరియు కారణాంక విభజన Ex 2.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 బహుపదులు మరియు కారణాంక విభజన Ex 2.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 బహుపదులు మరియు కారణాంక విభజన Ex 2.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 బహుపదులు మరియు కారణాంక విభజన Ex 2.5 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 2 బహుపదులు మరియు కారణాంక విభజన InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 3 జ్యామితీయ మూలాలు Ex 3.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 3 జ్యామితీయ మూలాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 సరళ రేఖలు మరియు కోణములు Ex 4.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 సరళ రేఖలు మరియు కోణములు Ex 4.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 సరళ రేఖలు మరియు కోణములు Ex 4.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 సరళ రేఖలు మరియు కోణములు Ex 4.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 4 సరళ రేఖలు మరియు కోణములు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 నిరూపక జ్యామితి Ex 5.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 నిరూపక జ్యామితి Ex 5.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 నిరూపక జ్యామితి Ex 5.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 5 నిరూపక జ్యామితి InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు Ex 6.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు Ex 6.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు Ex 6.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు Ex 6.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 6 రెండు చరరాశులలో రేఖీయ సమీకరణాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 త్రిభుజాలు Ex 7.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 త్రిభుజాలు Ex 7.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 త్రిభుజాలు Ex 7.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 త్రిభుజాలు Ex 7.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 7 త్రిభుజాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 చతుర్భుజాలు Ex 8.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 చతుర్భుజాలు Ex 8.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 చతుర్భుజాలు Ex 8.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 చతుర్భుజాలు Ex 8.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 8 చతుర్భుజాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 9 సాంఖ్యక శాస్త్రము Ex 9.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 9 సాంఖ్యక శాస్త్రము Ex 9.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 9 సాంఖ్యక శాస్త్రము InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు Ex 10.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 10 ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 వైశాల్యాలు Ex 11.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 వైశాల్యాలు Ex 11.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 వైశాల్యాలు Ex 11.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 11 వైశాల్యాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 వృత్తాలు Ex 12.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 వృత్తాలు Ex 12.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 వృత్తాలు Ex 12.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 వృత్తాలు Ex 12.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 వృత్తాలు Ex 12.5 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 12 వృత్తాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 13 జ్యామితీయ నిర్మాణాలు Ex 13.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 13 జ్యామితీయ నిర్మాణాలు Ex 13.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 13 జ్యామితీయ నిర్మాణాలు InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 14 సంభావ్యత Ex 14.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 14 సంభావ్యత InText Questions Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 గణితములో నిరూపణలు Ex 15.1 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 గణితములో నిరూపణలు Ex 15.2 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 గణితములో నిరూపణలు Ex 15.3 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 గణితములో నిరూపణలు Ex 15.4 Textbook Solutions PDF
- AP Board Class 9 Maths Chapter 15 గణితములో నిరూపణలు InText Questions Textbook Solutions PDF






0 Comments:
Post a Comment