AP Board Class 9 Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

AP Board Class 9 Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Book Answers

AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 9th Maths Chapter 7 Triangles Ex 7.1 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 9th Maths Chapter 7 Triangles Ex 7.1 book solutions pdf online from this page.

Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks Solutions PDF

Andhra Pradesh State Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 9th Maths Chapter 7 Triangles Ex 7.1 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks. These Andhra Pradesh State Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	9th
Subject	Maths
Chapters	Maths Chapter 7 Triangles Ex 7.1
Provider	Hsslive

How to download Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Answers.
Look for your Andhra Pradesh Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions for PDF Free.

AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.1

Question 1.
In quadrilateral ACBD, AC = AD and AB bisects ∠A. Show that ΔABC ≅ ΔABD What can you say about BC and BD ?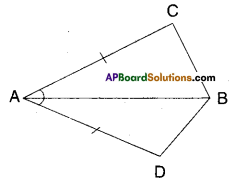

Solution:
Given that AC = AD
∠BAC = ∠BAD (∵ AB bisects∠A)
Now in ΔABC and ΔABD
AC = AD (∵ given)
∠BAC = ∠BAD (Y given)
AB = AB (common side)
∴ ΔABC ≅ ΔABD
(∵ SAS congruence rule)

Question 2.
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA, prove that i) ΔABD ≅ΔBAC ii) BD = AC
iii) ∠ABD = ∠BAC.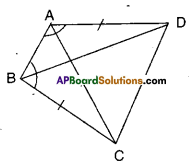

Solution :
i) Given that AD = BC and
∠DAB = ∠CBA
Now in ΔABD and ΔBAC
AB = AB (∵ Common side)
AD = BC (∵ given)
∠DAB = ∠CBA (∵ given)
∴ ΔABD ≅ ΔBAC
(∵ SAS congruence)
ii) From (i) AC = BD (∵ CPCT)
iii) ∠ABD = ∠BAC [ ∵ CPCT from (i)]

Question 3.
AD and BC are equal and perpendi-culars to a line segment AB. Show that CD bisects AB.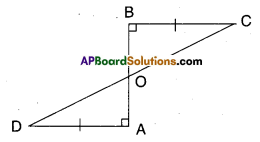

Solution:
Given that AD = BC; AD ⊥ AB; BC ⊥ AB
In ΔBOC and ΔAOD
∠BOC = ∠AOD (∵ vertically opposite angles)
∴ ΔOBC = ΔOAD (∵ right angle)
BC = AD
ΔOBC ≅ ΔOAD (∵ AAS congruence)
∴ OB = OA (∵ CPCT)
∴ ‘O’ bisects AB
Also OD = OC
∴ ‘O’ bisects CD
⇒ AB bisects CD

Question 4.
l and m are two parallel lines inter-sected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA.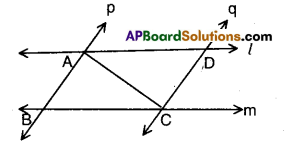

Solution:
Given that l // m; p // q.
In ΔABC and ΔCDA
∠BAC = ∠DCA (∵ alternate interior angles)
∠ACB = ∠CAD
AC = AC
∴ ΔABC ≅ ΔCDA (∵ ASA congruence)

Question 5.
In the figure given below AC = AE; AB = AD and ∠BAD = ∠EAC. Show that BC = DE.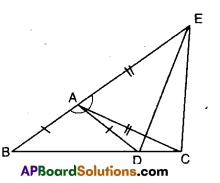

Solution:
Given that AC = AE, AB = AD and
∠BAD = ∠EAC
In ΔABC and ΔADE
AB = AD
AC = AE
∠BAD = ∠EAC
∴ ΔABC ≅ ΔADE (∵ SAS congruence)
⇒ BC = DE (CPCT)

Question 6.
In right triangle ABC, right angle is at ‘C’ M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that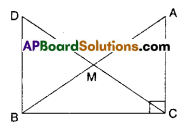

i) ΔAMC = ΔBMD
ii) ∠DBC is a right angle
iii) ΔDBC = ΔACB
iv) CM = 12 AB
Solution:
Given that ∠C = 90°
M is mid point of AB;
DM = CM (i.e., M is mid point of DC)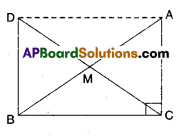

i) In ΔAMC and ΔBMD
AM = BM (∵ M is mid point of AB)
CM = DM ( ∵ M is mid point of CD)
∠AMC = ∠BMD ( ∵ Vertically opposite angles)
∴ ΔAMC ≅ ΔBMD
(∵ SAS congruence)

ii) ∠MDB = ∠MCA
(CPCT of ΔAMC and ΔBMD)
But these are alternate interior angles for the lines DB and AC and DC as transversal.
∴DB || AC
As AC ⊥ BC; DB is also perpendicular to BC.
∴ ∠DBC is a right angle.

iii) In ΔDBC and ΔACB
DB = AC (CPCT of ΔBMD and ΔAMC)
∠DBC = ∠ACB = 90°(already proved)
BC = BC (Common side)
∴ ΔDBC ≅ ΔACB (SAS congruence rule)

iv) DC = AB (CPCT of ΔDBC and ΔACB)
12 DC = 12 AB (Dividing both sides by 2)
CM = 12AB

Question 7.
In the given figure ΔBCD is a square and ΔAPB is an equilateral triangle.
Prove that ΔAPD ≅ ΔBPC.
[Hint: In ΔAPD and ΔBPC; 𝐀𝐃⎯⎯⎯⎯⎯⎯⎯⎯⎯=𝐁𝐂⎯⎯⎯⎯⎯⎯⎯⎯, 𝐀𝐏⎯⎯⎯⎯⎯⎯⎯⎯=𝐁𝐏⎯⎯⎯⎯⎯⎯⎯⎯ and ∠PAD = ∠PBC = 90° – 60° = 30°]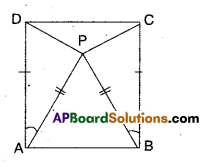

Solution:
Given that □ABCD is a square.
ΔAPB is an equilateral triangle.
Now in ΔAPD and ΔBPC
AP = BP ( ∵ sides of an equilateral triangle)
AD = BC (∵ sides of a square)
∠PAD = ∠PBC [ ∵ 90° – 60°]
∴ ΔAPD ≅ ΔBPC (by SAS congruence)

Question 8.
In the figure given below ΔABC is isosceles as 𝐀𝐁⎯⎯⎯⎯⎯⎯⎯⎯=𝐀𝐂⎯⎯⎯⎯⎯⎯⎯⎯⎯;𝐁𝐀⎯⎯⎯⎯⎯⎯⎯⎯ and 𝐂𝐀⎯⎯⎯⎯⎯⎯⎯⎯⎯ are produced to Q and P such that 𝐀𝐐⎯⎯⎯⎯⎯⎯⎯⎯⎯=𝐀𝐏⎯⎯⎯⎯⎯⎯⎯⎯. Show that 𝐏𝐁⎯⎯⎯⎯⎯⎯⎯⎯=𝐐𝐂⎯⎯⎯⎯⎯⎯⎯⎯⎯ .
(Hint: Compare ΔAPB and ΔACQ)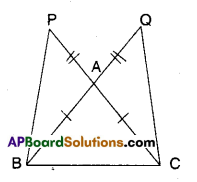

Solution:
Given that ΔABC is isosceles and
AP = AQ
Now in ΔAPB and ΔAQC
AP = AQ (given)
AB = AC (given)
∠PAB = ∠QAC (∵ Vertically opposite angles)
∴ ΔAPB ≅ ΔAQC (SAS congruence)
∴ 𝐏𝐁⎯⎯⎯⎯⎯⎯⎯⎯=𝐐𝐂⎯⎯⎯⎯⎯⎯⎯⎯⎯ (CPCT of ΔAPB and ΔAQC)

Question 9.
In the figure given below AABC, D is the midpoint of BC. DE ⊥ AB, DF ⊥ AC and DE = DF. Show that ΔBED ≅ AΔCFD.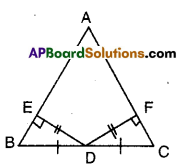

Solution:
Given that D is the mid point of BC of ΔABC.
DF ⊥ AC; DE = DF
DE ⊥ AB
In ΔBED and ΔCFD
∠BED = ∠CFD (given as 90°)
BD = CD (∵D is mid point of BC)
ED = FD (given)
∴ ΔBED ≅ ΔCFD (RHS congruence)

Question 10.
If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
Solution: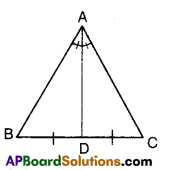

Let ΔABC be a triangle.
The bisector of ∠A bisects BC
To prove: ΔABC is isosceles
(i.e., AB = AC)
We know that bisector of vertical angle divides the base of the triangle in the ratio of other two sides.
∴ ABAC=BDBC
Thus ABAC = 1( ∵ given)
⇒ AB = AC
Hence the Triangle is isosceless.

Question 11.
In the given figure ΔABC is a right triangle and right angled at B such that ∠BCA = 2 ∠BAC. Show that the hypotenuse AC = 2BC.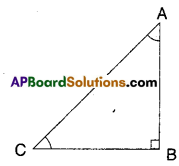

[Hint : Produce CB to a point D that BC = BD]
Solution: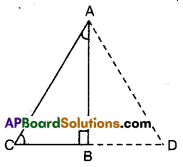

Given that ∠B = 90°; ∠BCA = 2∠BAC
To prove : AC = 2BC
Produce CB to a point D such that
BC = BD
Now in ΔABC and ΔABD
AB = AB (common)
BC = BD (construction)
∠ABC =∠ABD (∵ each 90°)
∴ ΔABC ≅ ΔABD
Thus AC = AD and ∠BAC = ∠BAD = 30° [CPCT]
[ ∵ If ∠BAC = x then
∠BCA = 2x
x + 2x = 90°
3x = 90°
⇒ x = 30°
∴ ∠ACB = 60°]
Now in ΔACD,
∠ACD = ∠ADC = ∠CAD = 60°
∴∠ACD is equilateral ⇒ AC = CD = AD
⇒ AC = 2BC (∵ C is mid point)

AP Board Textbook Solutions PDF for Class 9th Telugu

Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks for Exam Preparations

Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 exam preparation. The AP Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 9th Maths Chapter 7 Triangles Ex 7.1 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook Solutions

How to get AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook Answers??

Students can download the Andhra Pradesh Board Class 9 Maths Chapter 7 Triangles Ex 7.1 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 9th Maths Chapter 7 Triangles Ex 7.1, AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks, Andhra Pradesh State Board Class 9th Maths Chapter 7 Triangles Ex 7.1, Andhra Pradesh State Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbook solutions, AP Board Class 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks Solutions, Andhra Pradesh Board STD 9th Maths Chapter 7 Triangles Ex 7.1, AP Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks, Andhra Pradesh State Board STD 9th Maths Chapter 7 Triangles Ex 7.1, Andhra Pradesh State Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Textbook solutions, AP Board STD 9th Maths Chapter 7 Triangles Ex 7.1 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, July 14, 2022