AP Board Class 6 Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 15, 2023

AP Board Class 6 Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Book Answers

June 15, 2023 AP Board 6 Maths Solutions No comments

AP Board Class 6 Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Book Answers

AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 6th Maths Chapter 3 HCF and LCM InText Questions books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 6th Maths Chapter 3 HCF and LCM InText Questions book solutions pdf online from this page.

Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks Solutions PDF

Andhra Pradesh State Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 6th Maths Chapter 3 HCF and LCM InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks. These Andhra Pradesh State Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	6th
Subject	Maths
Chapters	Maths Chapter 3 HCF and LCM InText Questions
Provider	Hsslive

How to download Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Answers.
Look for your Andhra Pradesh Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions for PDF Free.

AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

Question 1.
How does the Sieve of Eratosthenes work ?
Solution:
The following example illustrates how the Sieve of Eratosthenes, can be used to find all the prime numbers that are less than 100. .
Step 1: Write the numbers from 1. to 100 in ten rows as shown below.
Step 2: Cross out 1 as 1 is neither a prime nor a composite number.
Step 3: Circle 2 and cross out all the multiples of 2. (2, 4, 6, 8, 10, 12, ………… )
Step 4: Circle 3 and cross out all the multiples of 3. (3, 6, 9, 12, 15, 18,………….)
Step 5: Circle 5 and cross out all the multiples of 5. (5, 10. 15, 20, 25……………… )
Step 6: Circle 7 and cross out all multiples of 7. (7, 14, 21. 28, 35, ………………….. )

Circle all the numbers that are not crossed out and they are the required prime numbers less than 100.

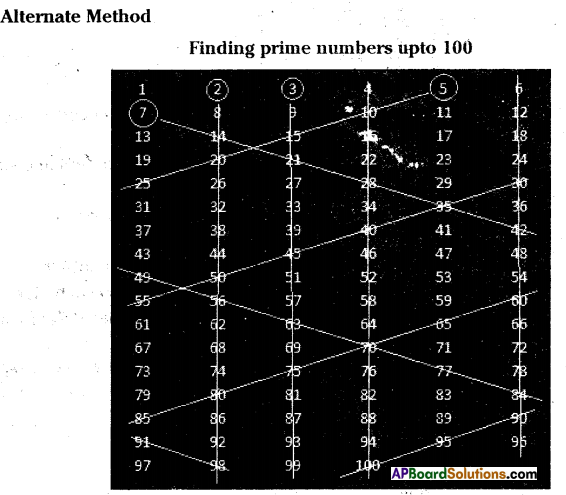
First arrange the numbers ffom 1 to 100 in a table as shown above.
Enter 6 numbers in each row until the last number 100 is reached.
First we select a number and we strike off all the multiples of it.
Start with 2 which is greater than 1.
Round off number 2 and strike off entire column until the end.
Similarly strike off 4th column and 6th column as they are divisible by 2.
Now round off next number 3 and strike off entire column until end.
The number 4 is already gone.

Now round off next number 5 and strike off numbers in inclined fashion as shown in the figure (they are all divisible by 5). When striking off ends in some row, start again striking off with number in another end which is divisible by 5. New striking off line should be parallel to previous strike off line as. shown in the figure.
The number 6 is already gone.
Now round off number 7 and strike off numbers as we did in case of number 5.
8,9,10 are also gone. .
Stop at this point.
Count all remaining numbers. Answer will be 25.

Prime numbers :
There are 25 prime numbers less than 100.
These are:

What if we go above 100 ? Around 400 BC the Greek mathematician. Euclid, proved that there are infinitely many prime numbers.

Co-primes: Two numbers are said to be co-prime if they have no factors in common. Example: (2, 9), (25, 28)
Any two consecutive numbers always form a pair of co-prime numbers.

Example:
Co-prime numbers are also called relatively prime number to one another.
Example: 3, 5, 8, 47 are relatively prime to one another/co-prime to each other.

Twin primes: Two prime numbers are said to be twin primes, if they differ by 2.
Example: (3, 5), (5, 7), (11, 13), …etc.

Prime factorization: The process of expressing the given number as the product of prime numbers is called prime factorization.
Example: Prime factorization of 24 is
24 = 2 x 12
= 2 x 2 x 6
= 2 x 2 x 2 x 3, this way is unique.

Every number can be expressed as product of primes in a unique manner. We can factorize a given number in to product of primes in two methods. They are
a) Division method
b) Factor tree method

Common factors: The set of all factors which divides all the given numbers are called their common factors.
Example: Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 & 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 & 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 & 48
Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
We can see that among their common factors 12 is the highest common factor. It is called H.C.F. of the given numbers. So H.C.F. of 24, 36 & 48 is 12.

H.C.F./G.C.D : The highest common factor or the greatest common divisor of given numbers is the greatest of their common factors.
H.C.F. of given two or more numbers can be found in two ways.
a) By prime factorization
b) By continued division
H.C.F. of any two consecutive numbers is always 1.
H.C.F. of relatively prime/co-prime numbers is always 1.
H.C.F. of any two consecutive even numbers is always 2.
H.C.F. of any two consecutive odd numbers is always 1.

Common multiples:
Multiples of 8: 8, 16, 24, 32, 40, 48,
Multiples of 12: 12, 24, 36, 48, … .
Multiples.common to 8 & 12: 24, 48; 72, 96, …
Least among the common multiple is 24. This is called L.C.M. of 8 & 12. The number of common multiples of given two or more numbers is infinite, as such greatest common multiple cannot be determined.

L.C.M.: The least common multiple of two or more numbers is the smallest natural number among their common multiples.
L.C.M. of given numbers can be found by the
a) Method of prime factorization.
b) Division method.
L.C.M. of any two consecutive numbers is always equal to their product.
L.C.M. of 8 &9 is 8 x 9 = 72
L.C.M. of co-prime numbers is always equal to their product.
L.C.M. of 8 & 15 is 8 x 15 = 120

Relation between the L.C.M. & H.C.F:
For a given two numbers Nj & N2 , the product of the numbers is equal to the product of their L.C.M.(L) & H.C.F.(H)
N₁ x N₂ = L x H

Check Your Progress (Page No. 29)

Question 1.
Are the numbers 900, 452, 9534, 788 divisible by 2? Why?
Solution:
Yes. Because these numbers have 0, 2, 4 and 8 in their ones place. The numbers having 0, 2, 4, 6 and 8 in their ones place are divisible by 2.

Question 2.
Are the numbers 953, 457, 781, 325, 269 divisible by 2? Why?
Solution:
No. Because, these numbers have 3, 7, 1, 5 and 9 in their ones place. The numbers having 0, 2,
4, 6 and 8 in their ones place are only divisible by 2. So, these are not divisible by 2.

Question 3.
Are the numbers 452, 673, 259, 356 divisible by 2? Verify.
Solution:
452 and 356 have 2 and 6 in their ones place respectively.
So, they are divisible by 2.
673 and 259 have 3 and 9 in their ones place respectively.
So, they are not divisible by 2.

Question 4.
Check whether the following numbers are divisible by 3 (using rule). Verify by actual division.
(i) 12345 (ii) 61392 (iii)8747
Solution:
i)12345
1 + 2 + 3 + 4 + 5=15 is a multiple of 3.
If the sum of the digits of a number is the multiple of 3, then the number is divisible by 3.
So, 12345 is divisible by 3.

ii) 61392
6 + 1 + 3 + 9 + 2 = 21is a multiple,of 3.
If the sum of the digits of a number is a multiple of 3, then the number is divisible
by 3.

So, 61392 is divisible by 3.

iii) 8747
8 + 7 + 4 + 7 = 26is not a multiple of 3.
If the sum of the digits of a number is a multiple of 3, then the numbei is divisible by 3. So, 8747 is not divisible by 3.

So, 8747 is not divisible by 3.

Let’s Explore (Page No. 29)

Question 1.
Is 8430 divisible by 6? Why?
Given number is 8430.
The given number has zero in the ones place.
So, 8430 is divisible by 2. –
And the unit sum is8 + 4 + 3 + 0 = 15 is a multiple of 3.
So, 8430 is divisible by 3.
If a number is divisible by both 2 and 3, then only it is divisible by 6.
8430 is divisible by both 2 and 3.
Therefore 8430 is divisible by 6.

Question 2.
Take any three 4 digit numbers and check whether they are divisible by 6.
Solution:
Consider: i) 5632, ii) 6855, iii) 9600 are three 4 digit numbers.
i) 5632 has 2 in its ones place. So, 5632 is divisible by 2.
The unit sum is
5 + 6 + 3 + 2 = 16 is not a multiple of 3. So, 5632 is not divisible by 3.
If a number is divisible by both 2 and 3, then only it is divisible by 6.
5632 is qnly divisible by 2, but not divisible by 3.
So, 5632 is not divisible by 6.

ii) 6855 has 5 in the ones place. So, 6855 is not divisible by 2.
6 + 8 + 5 + 5 = 24 is a multiple of 3.
So, 6855 is divisible by 3.
If a number is divisible by both 2 and 3, then only it is divisible by 6.
6855 is not divisible by 2, but it is divisible by 3.
So, 6855 is not divisible by 6.

iii) 9600 has ‘0’ in the ones place. So, 9600 is divisible by 2.
9 + 6 + 0 + 0 = 15 is a multiple of 3.
So, 9600 is divisible by 3. .
If a number is divisible by both 2 and 3, then only it is divisible by 6, 9600 is divisible by 1 both 2 and 3.
So, 9600 is divisible by 6.

Question 3.
Can you give an example of a number which is divisible by 6 but not by 2 and 3? Why?
Solution:
No. We can’t give any example, because if any number is divisible by both 2 and 3, then only it is divisible by 6. Otherwise it is not possible.

Check Your Progress (Page No. 30 & 31))

Question 1.
Test whether 6669 is divisible by 9. ,
Solution:
Given number is 6669.
Sum of the digits = 6 + 6 + 6 + 9 = 27 is divisible by 9
If the sum of the digits of a number is divisible by 9 then, it is divisible by 9. ” 27 is divisible by 9. So, 6669 is divisible by 9.

Question 2.
Without actual division, find whether 8989794 is divisible by 9.
Solution:
Given number is 8989794.
Sum of the digits =8+9+8+9+7+9+4=54 – 1
If the sum of the digits of a number is divisible by 9.
Then, it is divisible by 9.
54 is divisible by 9. So, 8989794 is divisible by 9.

Question 3.
Are the numbers 28570, 90875 divisible by 5? Verify by actual division also.
Solution:
a) Given number be 28570.
The numbers with zero or five at ones place are divisible by 5
28570 has zero in its ones place. So, 28570 is divisible by 5.
Actual division :

So, 28570 is completely divisible by 5.

b) Given number is 90875
In 90875, ones place digit is 5. So, 90875 is divisible by 5.
Actual division :

In the given number 90875 the digit in the units place is 5,
‘ So, it is divisible by 5.
So, 90875 is divisible by 5.

Question 4.
Check whether the number 598, 864, 4782 and 8976 are divisible by 4. Use divisibility rule and verify by actual division.
Solution:
a) Given number is 598.
The number formed by the digits in tens and ones places of 598 is 98.
If the number formed by last two digits (Ones and Tens) of the number is divisible
by 4, then the number is divisible by 4.
98 is not divisible by 4. So, 598 is not divisible by 4.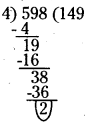

b) Given number is 864.
The number formed by tens and ones places of 864 is 64.
If the number formed by last two digits (ones and tens)
of the number is divisible by 4, then the number is divisible by 4.
64 is divisible by 4. So, 864 is divisible by 4.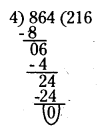

c) Given number is 4782.
The number formed by ones and tens places of 4782 is 82.
If the number formed by last two digits (ones and tens) of the number is divisible by 4, then the number is divisible by 4. 82 is not divisible by 4.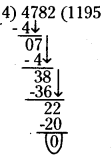

d) Given number is 8976.
The number formed by the digits in tens and ones places of 8976 is 76.
If the number formed by last two digits
(Tens and ones) of the number is divisible by 4. Then the number is divisible by 4.
76 is divisible by 4. So, 8976 is divisible by 4.

Question 1.
Fill the blanks and complete the table. (Page No. 32)
Solution: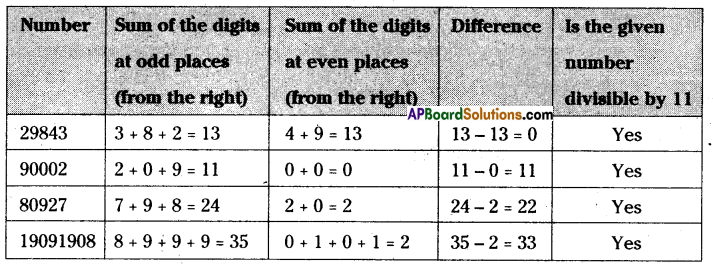

Lets Explore (Page No.33)

Question 1.
1221 is a polindrome number, which on reversing its digits gives the same number. Thus, every polindrome number with even number of digits is always divisible by 11. Write polindrome number of 6 – digits.
Solution:

There are some polindrome number of 6 – difits.

Check Your Progress (Page No.34)

Question 1.
Find the factors of 60.
Solution:
60 = 1 x 60
60 = 2 x 30
60 = 3 x 20
60 = 4 x 15
60 = 5 x 12
60 = 6 x 10
∴ The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Question 2.
Do all the factors of a given number divide the number exactly? Find the factors of 30 and verify by division.
30 = 1 x 30
30 = 3 x 10
30 = 2 x 15
30 = 5 x 6
The factors of 30 are 1, 2, 3, 5, 6,10, 15 and 30.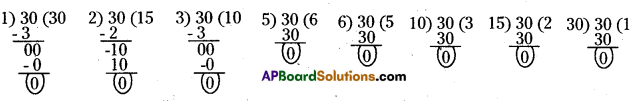

Yes, the factors of a given numbers are divide the number exactly.

Question 3.
3 is a factor of 15 and 24. Is 3 a factor of their difference also?
Solution:
Difference = 24 – 15 = 9 is the multiple of 3.
Yes, 3 is a factor of difference of 15 and 24.

Let’s Explore (Page No. 35)

Question 1.
What is the smallest prime number?
Solution:
2

Question 2.
What is the smallest composite number?
Solution:
4

Question 3.
What is the smallest odd prime number?
Solution:
3

Question 4.
What is the smallest odd composite number?
Solution:
9

Question 5.
Write 10 odd and 10 even composite numbers.
Solution:
Odd composite numbers are 9, 15, 21, 25, 27, 33, 35, 39, 45, 49.
Even composite numbers are 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.
Except 2, every even number is a composite number.

Let’s Explore (Page No. 36)

Question 1.
Can you guess a prime number which when on reversing its digits, gives another prime number? (Hint a 2 digit prime number)
Solution:
13 and 31; 17 and 71, 37 and 73 79 and 97.

Question 2.
311 is a prime number. Can you find the other two prime numbers just by rearrang-ing the digits?
Solution:
113, 131

Check Your Progress (Page No. 36)

Question 1.
From the following numbers identify different pairs of co-primes. 2, 3,4, 5,6,7, 8, 9 and 10.
Solution:
The numbers which have only 1 as the common factor are called co-primes, (or) Numbers having no common factors, other than 1 are called co-primes.
2,3; 2, 5; 2, 7; 2, 9; 3,4; 3, 5; 3, 7; 3, 8; 3,10; 4,5; 4, 7; 4, 9; 5, 6; 5, 7; 5,8; 5, 9; 6, 7; 8, 9 and 9,10. These are the different pairs of co-primes with 2, 3, 4, 5, 6, 7, 8, 9 and 10.
1) Any two primes always forms a pair of co-primes.
2) Any two consecutive numbers always form a pair of co-primes.
3) Any two primes cilways form a pair of co-primes. .

Question 2.
Write the pairs of twin primes less than 50.
Solution:
Two prime numbers are said to be twin primes, if they differ each other by 2.
Twin primes less than 50 are (3, 5); (5, 7); (11,13); (17, 19); (29, 31) and (41, 43).

(Page No. 36)

Question 1.
Find the HCF of 12, 16 and 28
Solution: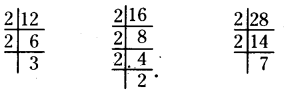

Thus 12 = 2 x 2 x 3
16 = 2 x 2 x 2 x 2
28 = 2 x 2 x 7
The common factor of 12, 16 and 28 ¡s 2 x 2 = 4.
Hence, H.C.F of 12, 16 and 28 is 4.

Let’s Explore (Page No. 40)

What is the HCF of any two
i) Consecutive numbers ?
ii) Consecutive even numbers ?
iii) Consecutive odd numbers? What do you observe? Discuss with your Mends.
Solution:
Consider the two consecutive number are 5, 6 and 9, 10.

We observed that HCF of any two consecutive numbers is always 1.

ii) Consider two consecutive even numbers are 8, 10 and 20, 22.

We observed that HCF of any two consecutive even numbers is always 2.

iii)Consider the consecutive odd numbers are 7, 9 and 13, 15.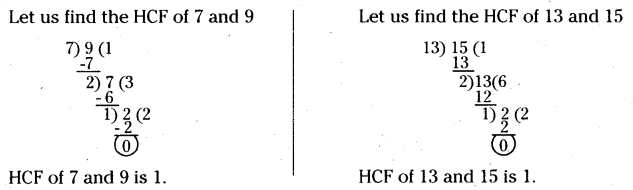

We observed that HCF of any two consecutive odd numbers is always 1.

(Page No. 42)

Question 1.
Find LCM of (i) 3, 4 (ii) 10, 11 (iii) 10, 30 (iv) 12, 24 (v) 3, 12 by prime factorization method.
Solution:
i) Given numbers are 3, 4
Factors of 3 = 1 x 3
Factors of 4 = 2 x 2
LCM of 3, 4 = 1 x 3 x 2 x 2 = 12

ii) Given numbers are 10, 11
Factors of 10 = 2 x 5
Factors of 11 = 1 x 11
LCM of 10, 11 = 2 x 5 x 11 = 110

iii) Given numbers are 10, 30
Factors of 10 = 2×5
Factors of 30 = 2x3x5
LCM of 10, 30 = 2 x 3 x 5 = 30

iv) Given numbers are 12, 24
Factors of 12 = 2x2x3 ,
Factors of 24 =. 2 x 2 x 2 x 3
LCM of 12, 24 = 2 x 2 x 2 x 3 = 24

v) Given numbers are 3,12 Factors of 3 = 1×3
Factors of 12 =2 x 2 x 3,
LCM of 3, 12 = 3 x 2 x 2 = 12

(Page No. 43)

Question 1.
What is the LCM and HCF of twin prime numbers ?
Solution:
LCM = Product of the taken twin primes and HCF = 1

AP Board Textbook Solutions PDF for Class 6th Maths

Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks for Exam Preparations

Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions can be of great help in your Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions exam preparation. The AP Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 6th Maths Chapter 3 HCF and LCM InText Questions Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook Solutions

How to get AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook Answers??

Students can download the Andhra Pradesh Board Class 6 Maths Chapter 3 HCF and LCM InText Questions Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 6th Maths Chapter 3 HCF and LCM InText Questions, AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks, Andhra Pradesh State Board Class 6th Maths Chapter 3 HCF and LCM InText Questions, Andhra Pradesh State Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbook solutions, AP Board Class 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks Solutions, Andhra Pradesh Board STD 6th Maths Chapter 3 HCF and LCM InText Questions, AP Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks, Andhra Pradesh State Board STD 6th Maths Chapter 3 HCF and LCM InText Questions, Andhra Pradesh State Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Textbook solutions, AP Board STD 6th Maths Chapter 3 HCF and LCM InText Questions Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 15, 2023