AP Board Class 6 Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions PDF: Download Andhra Pradesh Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Book Answers

AP Board Class 6 Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions PDF: Download Andhra Pradesh Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Book Answers

AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise book solutions pdf online from this page.

Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks Solutions PDF

Andhra Pradesh State Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks. These Andhra Pradesh State Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	6th
Subject	Maths
Chapters	Maths Chapter 7 Introduction to Algebra Unit Exercise
Provider	Hsslive

How to download Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions Answers PDF Online?

1. Visit our website - Hsslive
2. Click on the Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Answers.
3. Look for your Andhra Pradesh Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks PDF.
4. Now download or read the Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions for PDF Free.

AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

Question 1.
The cost of one fan is Rs. 1500. Then what is the cost of ‘n’ fans?
Answer: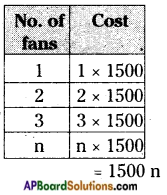

Given cost of one fan = Rs. 1500
Number of fans = n
Cost of n fans = cost of one fan × no. of fans = 1500 × n
∴ Cost of n fans = 1500n

Question 2.
Srinu has number of pencils. Raheem has 4 times the pencils as of Srinu. How many pencils does Rahim has? Write an expression.
Answer:
Let number of pencils Srinu has = x
Number of pencils Raheem has = 4 times of Srinu
= 4 × x
∴ Number of pencils Raheem has = 4x

Question 3.
Parvathi has 5 more books than Sofia. How many books are with Parvathi? Write an expression choosing any variable for number of books.
Answer:
Let number of books Sofia has = y
Given Parvathi has 5 more books than Sofia
Number of books Parvathi has = 5 books more than Sofia
= y + 5
∴ Number of books Parvathi has = y + 5

Question 4.
Which of the following are equations?
i) 10 – 4p = 2
ii) 10 + 8x < – 22
iii) x + 5 = 8
iv) m + 6 = 2
v) 22x – 5 = 8
vi) 4k + 5 > – 100
vii) 4p + 7 = 23
viii) y < – 4
Answer:
i) 10 – 4p = 2
We know that, a mathematical statement involving equality symbol is called an equation.
10 – 4p = 2 has equality symbol.
So, it is an equation.

ii) 10 + 8x < – 22
We know that, a mathematical statement involving equality symbol is called an equation.
10 + 8x < – 22 has no equality symbol.
So, it is not an equation [so it is an inequation]

iii) x + 5 = 8 We know that, a mathematical statement involving equality symbol is called an equation.
x + 5 = 8 has equality symbol.
So, it is an equation.

iv) m + 6 = 2 We know that, a mathematical statement involving equality symbol is called an equation.
m + 6 = 2 has equality symbol.
So, it is an equation.

v) 22x – 5 = 8 We know that, a mathematical statement involving equality symbol is called an equation.
22x – 5 = 8 has equality symbol.
So, it is an equation.

vi) 4k + 5 > – 100
We know that, a mathematical statement involving equality symbol is called an equation.
4k + 5 > -100 has no equality symbol.
So, it is not an equation.
It is an inequation.

vii) 4p + 7 = 23
We know that, a mathematical statement involving equality symbol is ailed an equation.
4p + 7 = 23 has equality symbol.
So, it is an equation.

viii) y < – 4
We know that, a mathematical statement involving equality symbol is called an equation.
y < – 4 has no equality symbol.
So, it is not an equation.
It is an inequation.

Question 5.
Write L.H.S and R.H.S of the following equations:
i) 7x + 8 = 22
ii) 9y – 3 = 6
iii) 3k – 10 = 2
iv) 3p – 4q = -19
Answer:
i) 7x + 8 = 22
Given equation is 7x + 8 = 22
LHS = 7x + 8
RHS = 22

ii) 9y – 3 = 6
Given equation is 9y – 3 = 6
LHS = 9y – 3
RHS = 6

iii) 3k – 10 = 2
Given equation is 3k – 10 = 2
LHS = 3k – 10
RHS = 2

iv) 3p – 4q = -19
Given equation is 3p – 4q = -19
LHS = 3p – 4q
RHS = -19

Question 6.
Solve the following equations by trial and error method.
i) x – 3 = 5
ii) y + 6 = 15
iii) y = -1
iv) 2k – 1 = 3
Answer:
i) x – 3 = 5
Given equation is x – 3 = 5
If x = 1, then the value of x – 3 = 1 – 3 = -2 ≠ 5
If x = 2, then the value of x – 3 = 2 – 3 = -l ≠ 5
If x = 3, then the value of x – 3 = 3 – 3 = 0 ≠ 5
If x = 4, then the value of x – 3 = 4 – 3 = l ≠ 5
If x = 5, then the value of x – 3 = 5 – 3 = 2 ≠ 5
If x = 6, then the value of x – 3 = 6 – 3 = 3 ≠ 5
If x = 7, then the value of x – 3 = 7 – 3 = 4 ≠ 5
If x = 8, then the value of x – 3 = 8 – 3 = 5 = 5
From the above when x = 8, the both LHS and RHS are equal.
∴ Solution of the equation x – 3 = 5 is x = 8

ii) y + 6 = 15
Given equation is y + 6 = 15
If y = 1, then the value of y + 6 = 1 + 6 = 7 ≠ 15
If y = 2, then the value of y + 6 = 2 + 6 = 8 ≠ 15
If y = 3, then the value of y +6 = 3 + 6 = 9 ≠ 15
If y = 4, then the value of y + 6 = 4 + 6 = 10 ≠ 15
If y = 5, then the value of y + 6 = 5 + 6 = 11 ≠ 15
If y = 6, then the value of y + 6 = 6 + 6 = 12 ≠ 15
If y = 7, then the value hf y + 6 = 7 + 6 = 13 ≠ 15
If y = 8, then the value of y + 6 = 8 + 6 = 14 ≠ 15
If y = 9, then the value of y + 6 = 9 + 6 = 15 = 15
From the above when y = 9, the both LHS and RHS are equal.
∴ Solution of the equation y + 6 = 15 is y = 9

iii) 𝑚2 = -1
Given equation is 𝑚2 = -1
If m = 1, then the value of 𝑚2 = 12 ≠ -1
If m = 2, then the value of 𝑚2 = 22 = 1 ≠ -1
If m = 3, then the value of 𝑚2 = 32 ≠ -1
Here, we are not getting negative values.
If we take (substitute) m as a negative number we will get negative value.
If m = -1, then the value of 𝑚2 = −12 ≠ -1
If m = -2, then the value of 𝑚2 = −22 = -1 = -1
From the above when m = -2, the both LHS and RHS are equal.
∴ Solution of the equation 𝑚2 = -1 is m = -2.

iv) 2k – 1 = 3
Given equation is 2k – 1 = 3
If k = 1, then the value of 2k – 1 = 2(1) – 1 = 2 – 1 = 1 ≠ 3
If k = 2, then the value of 2k – 1 = 2(2) – 1 = 4 – 1 = 3 = 3
From the above when k – 2, the both LHS and RHS are equal.
Solution of the equation 2k – 1 = 3 is k = 2.

AP Board Textbook Solutions PDF for Class 6th Maths

• AP Board Class 6
• AP Board Class 6 Maths
• AP Board Class 6 Maths Chapter 1 Numbers All Around us Ex 1.1
• AP Board Class 6 Maths Chapter 1 Numbers All Around us Ex 1.2
• AP Board Class 6 Maths Chapter 1 Numbers All Around us Ex 1.3
• AP Board Class 6 Maths Chapter 1 Numbers All Around us Ex 1.4
• AP Board Class 6 Maths Chapter 1 Numbers All Around us Unit Exercise
• AP Board Class 6 Maths Chapter 1 Numbers All Around us InText Questions
• AP Board Class 6 Maths Chapter 2 Whole Numbers Ex 2.1
• AP Board Class 6 Maths Chapter 2 Whole Numbers Ex 2.2
• AP Board Class 6 Maths Chapter 2 Whole Numbers Ex 2.3
• AP Board Class 6 Maths Chapter 2 Whole Numbers Unit Exercise
• AP Board Class 6 Maths Chapter 2 Whole Numbers InText Questions
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.1
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.2
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.3
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.4
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.5
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.6
• AP Board Class 6 Maths Chapter 3 HCF and LCM Ex 3.7
• AP Board Class 6 Maths Chapter 3 HCF and LCM Unit Exercise
• AP Board Class 6 Maths Chapter 3 HCF and LCM InText Questions
• AP Board Class 6 Maths Chapter 4 Integers Ex 4.1
• AP Board Class 6 Maths Chapter 4 Integers Ex 4.2
• AP Board Class 6 Maths Chapter 4 Integers Ex 4.3
• AP Board Class 6 Maths Chapter 4 Integers Ex 4.4
• AP Board Class 6 Maths Chapter 4 Integers Unit Exercise
• AP Board Class 6 Maths Chapter 4 Integers InText Questions
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals Ex 5.1
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals Ex 5.2
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals Ex 5.3
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals Ex 5.4
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals Ex 5.5
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals Unit Exercise
• AP Board Class 6 Maths Chapter 5 Fractions and Decimals InText Questions
• AP Board Class 6 Maths Chapter 6 Basic Arithmetic Ex 6.1
• AP Board Class 6 Maths Chapter 6 Basic Arithmetic Ex 6.2
• AP Board Class 6 Maths Chapter 6 Basic Arithmetic Ex 6.3
• AP Board Class 6 Maths Chapter 6 Basic Arithmetic Ex 6.4
• AP Board Class 6 Maths Chapter 6 Basic Arithmetic Unit Exercise
• AP Board Class 6 Maths Chapter 6 Basic Arithmetic InText Questions
• AP Board Class 6 Maths Chapter 7 Introduction to Algebra Ex 7.1
• AP Board Class 6 Maths Chapter 7 Introduction to Algebra Ex 7.2
• AP Board Class 6 Maths Chapter 7 Introduction to Algebra Ex 7.3
• AP Board Class 6 Maths Chapter 7 Introduction to Algebra Unit Exercise
• AP Board Class 6 Maths Chapter 7 Introduction to Algebra InText Questions
• AP Board Class 6 Maths Chapter 8 Basic Geometric Concepts Ex 8.1
• AP Board Class 6 Maths Chapter 8 Basic Geometric Concepts Ex 8.2
• AP Board Class 6 Maths Chapter 8 Basic Geometric Concepts Ex 8.3
• AP Board Class 6 Maths Chapter 8 Basic Geometric Concepts Ex 8.4
• AP Board Class 6 Maths Chapter 8 Basic Geometric Concepts Unit Exercise
• AP Board Class 6 Maths Chapter 8 Basic Geometric Concepts InText Questions
• AP Board Class 6 Maths Chapter 9 2D-3D Shapes Ex 9.1
• AP Board Class 6 Maths Chapter 9 2D-3D Shapes Ex 9.2
• AP Board Class 6 Maths Chapter 9 2D-3D Shapes Ex 9.3
• AP Board Class 6 Maths Chapter 9 2D-3D Shapes Ex 9.4
• AP Board Class 6 Maths Chapter 9 2D-3D Shapes Unit Exercise
• AP Board Class 6 Maths Chapter 9 2D-3D Shapes InText Questions
• AP Board Class 6 Maths Chapter 10 Practical Geometry Ex 10.1
• AP Board Class 6 Maths Chapter 10 Practical Geometry Ex 10.2
• AP Board Class 6 Maths Chapter 10 Practical Geometry Ex 10.3
• AP Board Class 6 Maths Chapter 10 Practical Geometry Ex 10.4
• AP Board Class 6 Maths Chapter 10 Practical Geometry Unit Exercise
• AP Board Class 6 Maths Chapter 10 Practical Geometry InText Questions
• AP Board Class 6 Maths Chapter 11 Perimeter and Area Ex 11.1
• AP Board Class 6 Maths Chapter 11 Perimeter and Area Ex 11.2
• AP Board Class 6 Maths Chapter 11 Perimeter and Area Ex 11.3
• AP Board Class 6 Maths Chapter 11 Perimeter and Area Unit Exercise
• AP Board Class 6 Maths Chapter 11 Perimeter and Area InText Questions
• AP Board Class 6 Maths Chapter 12 Data Handling Ex 12.1
• AP Board Class 6 Maths Chapter 12 Data Handling Ex 12.2
• AP Board Class 6 Maths Chapter 12 Data Handling Ex 12.3
• AP Board Class 6 Maths Chapter 12 Data Handling Unit Exercise
• AP Board Class 6 Maths Chapter 12 Data Handling InText Questions
• AP Board Class 6 Maths Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు Ex 1.1
• AP Board Class 6 Maths Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు Ex 1.2
• AP Board Class 6 Maths Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు Ex 1.3
• AP Board Class 6 Maths Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు Ex 1.4
• AP Board Class 6 Maths Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు Unit Exercise
• AP Board Class 6 Maths Chapter 1 మన చుట్టూ ఉండే సంఖ్యలు InText Questions
• AP Board Class 6 Maths Chapter 2 పూర్ణాంకాలు Ex 2.1
• AP Board Class 6 Maths Chapter 2 పూర్ణాంకాలు Ex 2.2
• AP Board Class 6 Maths Chapter 2 పూర్ణాంకాలు Ex 2.3
• AP Board Class 6 Maths Chapter 2 పూర్ణాంకాలు Unit Exercise
• AP Board Class 6 Maths Chapter 2 పూర్ణాంకాలు InText Questions
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.1
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.2
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.3
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.4
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.5
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.6
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Ex 3.7
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు Unit Exercise
• AP Board Class 6 Maths Chapter 3 గ.సా.కా – క.సా.గు InText Questions
• AP Board Class 6 Maths Chapter 4 పూర్ణసంఖ్యలు Ex 4.1
• AP Board Class 6 Maths Chapter 4 పూర్ణసంఖ్యలు Ex 4.2
• AP Board Class 6 Maths Chapter 4 పూర్ణసంఖ్యలు Ex 4.3
• AP Board Class 6 Maths Chapter 4 పూర్ణసంఖ్యలు Ex 4.4
• AP Board Class 6 Maths Chapter 4 పూర్ణసంఖ్యలు Unit Exercise
• AP Board Class 6 Maths Chapter 4 పూర్ణసంఖ్యలు InText Questions
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలుs Ex 5.1
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు Ex 5.2
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు Ex 5.3
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు Ex 5.4
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు Ex 5.5
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు Unit Exercise
• AP Board Class 6 Maths Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు InText Questions
• AP Board Class 6 Maths Chapter 6 ప్రాథమిక అంకగణితం Ex 6.1
• AP Board Class 6 Maths Chapter 6 ప్రాథమిక అంకగణితం Ex 6.2
• AP Board Class 6 Maths Chapter 6 ప్రాథమిక అంకగణితం Ex 6.3
• AP Board Class 6 Maths Chapter 6 ప్రాథమిక అంకగణితం Ex 6.4
• AP Board Class 6 Maths Chapter 6 ప్రాథమిక అంకగణితం Unit Exercise
• AP Board Class 6 Maths Chapter 6 ప్రాథమిక అంకగణితం InText Questions
• AP Board Class 6 Maths Chapter 7 బీజ గణిత పరిచయం Ex 7.1
• AP Board Class 6 Maths Chapter 7 బీజ గణిత పరిచయం Ex 7.2
• AP Board Class 6 Maths Chapter 7 బీజ గణిత పరిచయం Ex 7.3
• AP Board Class 6 Maths Chapter 7 బీజ గణిత పరిచయం Unit Exercise
• AP Board Class 6 Maths Chapter 7 బీజ గణిత పరిచయం InText Questions
• AP Board Class 6 Maths Chapter 8 జ్యామితీయ భావనలు Ex 8.1
• AP Board Class 6 Maths Chapter 8 జ్యామితీయ భావనలు Ex 8.2
• AP Board Class 6 Maths Chapter 8 జ్యామితీయ భావనలు Ex 8.3
• AP Board Class 6 Maths Chapter 8 జ్యామితీయ భావనలు Ex 8.4
• AP Board Class 6 Maths Chapter 8 జ్యామితీయ భావనలు Unit Exercise
• AP Board Class 6 Maths Chapter 8 జ్యామితీయ భావనలు InText Questions
• AP Board Class 6 Maths Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Ex 9.1
• AP Board Class 6 Maths Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Ex 9.2
• AP Board Class 6 Maths Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Ex 9.3
• AP Board Class 6 Maths Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Ex 9.4
• AP Board Class 6 Maths Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు Unit Exercise
• AP Board Class 6 Maths Chapter 9 ద్విమితీయ – త్రిమితీయ ఆకారాలు InText Questions
• AP Board Class 6 Maths Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.1
• AP Board Class 6 Maths Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.2
• AP Board Class 6 Maths Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.3
• AP Board Class 6 Maths Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.4
• AP Board Class 6 Maths Chapter 10 ప్రాయోజిక జ్యామితి Unit Exercise
• AP Board Class 6 Maths Chapter 10 ప్రాయోజిక జ్యామితి InText Questions
• AP Board Class 6 Maths Chapter 11 చుట్టుకొలత – వైశాల్యం Ex 11.1
• AP Board Class 6 Maths Chapter 11 చుట్టుకొలత – వైశాల్యం Ex 11.2
• AP Board Class 6 Maths Chapter 11 చుట్టుకొలత – వైశాల్యం Unit Exercise
• AP Board Class 6 Maths Chapter 11 చుట్టుకొలత – వైశాల్యం InText Questions
• AP Board Class 6 Maths Chapter 12 దత్తాంశ నిర్వహణ Ex 12.1
• AP Board Class 6 Maths Chapter 12 దత్తాంశ నిర్వహణ Ex 12.2
• AP Board Class 6 Maths Chapter 12 దత్తాంశ నిర్వహణ Ex 12.3
• AP Board Class 6 Maths Chapter 12 దత్తాంశ నిర్వహణ Unit Exercise
• AP Board Class 6 Maths Chapter 12 దత్తాంశ నిర్వహణ InText Questions

Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks for Exam Preparations

Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions can be of great help in your Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise exam preparation. The AP Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Solutions

How to get AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook Answers??

Students can download the Andhra Pradesh Board Class 6 Maths Chapter 7 Introduction to Algebra Unit Exercise Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise, AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks, Andhra Pradesh State Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise, Andhra Pradesh State Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook solutions, AP Board Class 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks Solutions, Andhra Pradesh Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise, AP Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks, Andhra Pradesh State Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise, Andhra Pradesh State Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbook solutions, AP Board STD 6th Maths Chapter 7 Introduction to Algebra Unit Exercise Textbooks Solutions,