 |
| AP Board Class 7 Maths Chapter 8 Exponents and Powers InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 7th Maths Chapter 8 Exponents and Powers InText Questions Book Answers |
Andhra Pradesh Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Textbooks Solutions PDF
Andhra Pradesh State Board STD 7th Maths Chapter 8 Exponents and Powers InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 7th Maths Chapter 8 Exponents and Powers InText Questions Textbooks. These Andhra Pradesh State Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 7th |
| Subject | Maths |
| Chapters | Maths Chapter 8 Exponents and Powers InText Questions |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Answers.
- Look for your Andhra Pradesh Board STD 7th Maths Chapter 8 Exponents and Powers InText Questions Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Textbook Solutions for PDF Free.
AP Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 7th Maths Chapter 8 Exponents and Powers InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:Question 1.
Write the following in exponential form by using 10 as the base number :
(i) 10,00,00,000
(ii) 100,00,00,000
Answer:
| Number | Expanded form | Exponential |
| (i) 10,00,00,000 | 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 | 108 |
| (ii) 100,00,00,000 | 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 | 109 |
Let’s Explore [Page No. 29]
Question 1.
Observe and complete the following table. First one is done for you.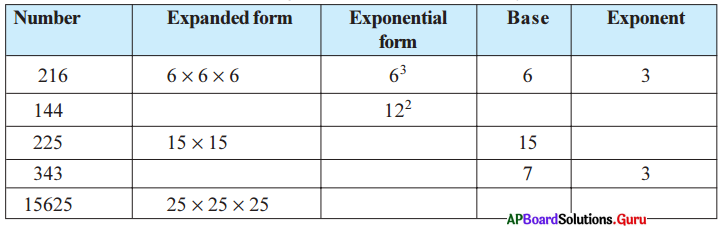
Answer: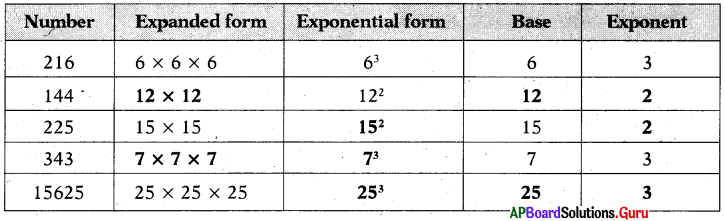
Question 2.
Write the following numbers in exponential form. Also state the base, exponent and how to read. .
(i) 16
(ii) 49
(iii) 512
(iv) 243
Answer: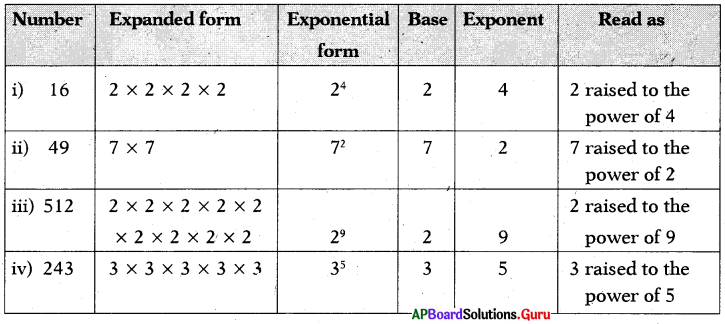
Question 3.
Compute the following and write the greater one.
(i) 43 or 34
Answer:
43 = 4 × 4 × 4 = 64
34 = 3 × 3 × 3 × 3 = 81 is greater.
64 < 81 (or) 81 > 64
So, 43 < 34 (or) 34 > 43
(ii) 53 or 35
Answer:
53 = 5 × 5 × 5 = 125
35 = 3 × 3 × 3 × 3 × 3 = 243 is greater.
125 < 243 (or) 243 > 125
So, 53 < 35 (or) 35 > 53
Question 4.
Is 32 equal to 23 ? Justify your answer.
Answer:
32 = 3 × 3 = 9
23 = 2 × 2 × 2 = 8
9 ≠ 8
32 ≠ 23
So, ab ≠ ba unless a = b
Check Your Progress [Page No. 30]
Express the following number in exponential form using prime factorisation:
(i) 432
Answer:
432 = 2 × 216
= 2 × 2 × 108
= 2 × 2 × 2 × 54
= 2 × 2 × 2 × 2 × 27
= 2 × 2 × 2 × 2 × 3 × 9
= 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ 432 = 24 × 33
(ii) 1296
Answer:
1296 = 2 × 648
= 2 × 2 × 324
= 2 × 2 × 2 × 162
= 2 × 2 × 2 × 2 × 81
= 2 × 2 × 2 × 2 × 3 × 27
= 2 × 2 × 2 × 2 × 3 × 3 × 9
= 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
∴ 1296 = 24 × 34
(iii) 729
Answer: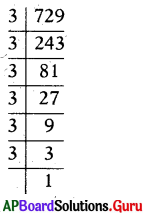
729 = 3 × 243
= 3 × 3 × 81
= 3 × 3 × 3 × 27
= 3 × 3 × 3 × 3 × 9
= 3 × 3 × 3 × 3 × 3 × 3
729 = 36
(iv) 1600
Answer:
1600 = 2 × 800
= 2 × 2 × 400
= 2 × 2 × 2 × 200
= 2 × 2 × 2 × 2 × 100
= 2 × 2 × 2 × 2 × 2 × 50
= 2 × 2 × 2 × 2 × 2 × 2 × 25
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
1600 = 26 × 52
Let’s Explore [Page No. 32]
Question 1.
Write the appropriate number in place of ▢ in the following.
Let ‘b’ be any non-zero integer.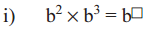
Answer: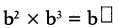
= b2 × b3
= b × b × b × b × b = b5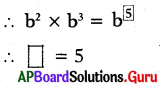
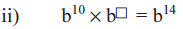
Answer: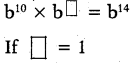
then b10 × b1 = b14
b10+1 = b14
b11 ≠ b14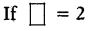
then b10 × b2 = b14
b10+2 = b14
b12 ≠ b14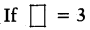
then b10 × b3 = b14
b10+3 = b14
b13 ≠ b14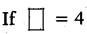
then b10 × b4 = b14
b10+4 = b14
∴ b14 = b14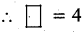
Question 2.
Simplify the following using the formula am × an = am+n
(i) 57 × 54
Answer:
57 × 54
We know that am × an = am+n;
57 × 54 = 57+4 = 511
∴ 57 × 54 = 511
(ii) p3 × p2
Answer:
p3 × p2
We know that am × an = am+n
p3 × p2 = p3+2 = p5
∴ p3 × p2 = p5
(iii) (-4)10 × (-4)3 × (-4)2
Answer:
(-4)10 × (-4)3 × (-4)2
We know that am × an = am+n
(- 4)10+3+2 = (- 4)15
∴ (-4)10 × (-4)3 × (-4)2 = (- 4)15
Let’s Explore [Page No. 33]
Question 1.
Write the following in exponential form using the formula (am)n = amn.
(i) (62)4
Answer:
(62)4
We know (am)n = amn
(62)4 = 62×4 = 68
∴ (62)4 = 68
(ii) (22)100
Answer:
(22)100
We know (am)n = amn
(22)100 = 22×100 = 2200
∴ (22)100 = 2200
(iii) (206)2
Answer:
(206)2
We know (am)n = amn
(206)2 = 206×2 = 2012
∴ (206)2 = 2012
(iv) [(-10)3]5
Answer:
[(-10)3]5
We know (am)n = amn
[(-10)3]5 =(-10)3×5 = (-10)15
∴ [(- 10)3]5 = (- 10)15
Check Your Progress [Page No. 34]
Simplify the following by using the law , am × bm = (ab)m.
(i) 76 × 36
Answer:
76 × 36
We know, am × bm = (ab)m
76 × 36 = (7 × 3)6 = (21)6
∴ 76 × 36 = 216
(ii) (3 × 5)4
Answer:
(3 × 5)4
We know, (ab)m = am × bm
(3 × 5)4 = 34 × 54
∴ (3 × 5)4 = 34 × 54
(iii) a4 × b4
Answer:
a4 × b4
We know, am × bm = (ab)m
a4 × b4 = (a . b)4
∴ a4 × b4 = (a . b)4
(iv) 32 × a2
Answer:
32 × a2
We know, am × bm = (ab)m
32 × a2 = (3 × a)2 = (3a)2
∴ 32 × a2 = (3a)2
Let’s Explore [Page No. 37]
Question 1.
Simplify and write In the form of am-n Or 1𝐚𝐧−𝐦
(i) 108104
Answer:
We Know 108104 = am-n
108104 = 108-4 = 104
∴108104 = 104
(ii) (−7)13(−7)10
Answer:
(−7)13(−7)10
We Know 𝑎𝑚𝑎𝑛 = am-n (m > n)
(−7)13(−7)10 = (-7)13-10
= (-7)3 = -7 × -7 × -7 = – 343
∴(−7)13(−7)10 = – 343
(iii) 125128
Answer:
(iv) 3437
Answer:
Question 2.
Fill the appropriate number In the box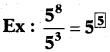
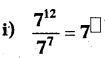
Answer: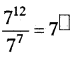
We Know 𝑎𝑚𝑎𝑛 = am-n (m > n)
71277 = 712-7 = 75
∴ 71277 = 75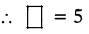
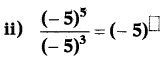
Answer: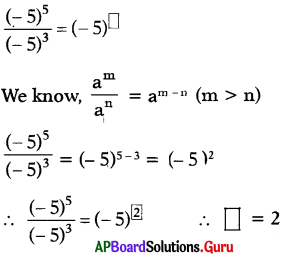
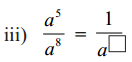
Answer:
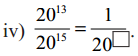
Answer:
Question 3.
Simplify the following :
(i) 6868
Answer:
6868
We Know 𝑎𝑚𝑎𝑛 = am-n
6868 = 68-8 = 60 = 1 (∵ a0 = 1)
(ii) 𝑡10𝑡10
Answer:
𝑡10𝑡10
We Know 𝑎𝑚𝑎𝑛 = am-n
𝑡10𝑡10 = t10-10 = t0 = 1 (∵ a0 = 1)
(iii) 127127
Answer:
127127
We Know 𝑎𝑚𝑎𝑛 = am-n
127127 = 127-7 = 120 = 1 (∵ a0 = 1)
(iv) 𝑝5𝑝5
Answer:
𝑝5𝑝5
We Know 𝑎𝑚𝑎𝑛 = am-n
𝑝5𝑝5 = p10-10 = p0 = 1 (∵ a0 = 1)
Check Your Progress [Page No. 38]
Question 1.
Complete the following boxes .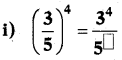
Answer:
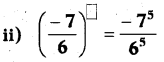
Answer:
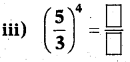
Answer:
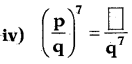
Answer:
Check Your Progress [Page No. 39]
Question 1.
Express the following in exponential form.
(i) −27125
Answer:
(ii) −32243
Answer:
(iii) −1251000
Answer:
(iv) −1625
Answer:
Let’s Think [Page No. 39]
Question 1.
Deekshltha and Harsha computed 4(3)2 in different ways.
Deeksbitha did it like this
4(3)2 = (4 × 3)2
= 122
= 144
Harsha did it like this
4(3)2 = 4 × (3 × 3)
= 4 × 9
= 36
Who has done the problem Incorrectly?
Discuss the reason for the mistake with your friends.
Answer:
In 4(3)2 square only belongs to 3, but not 4.
So, Deekshitha did wrong and Harsha did correct.
Let’s Do Activity [Page No. 40]
Finding the pair : Divide the classroom into two groups. Each group has a set of cards. Each student of group 1 has to pair with one suitable student of group 2 by stating in the reason.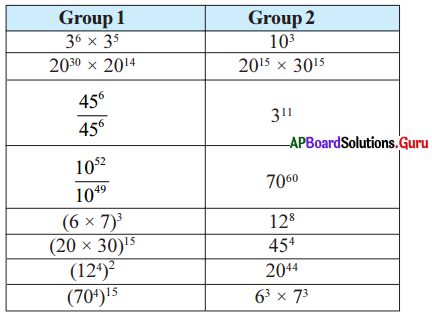
Answer: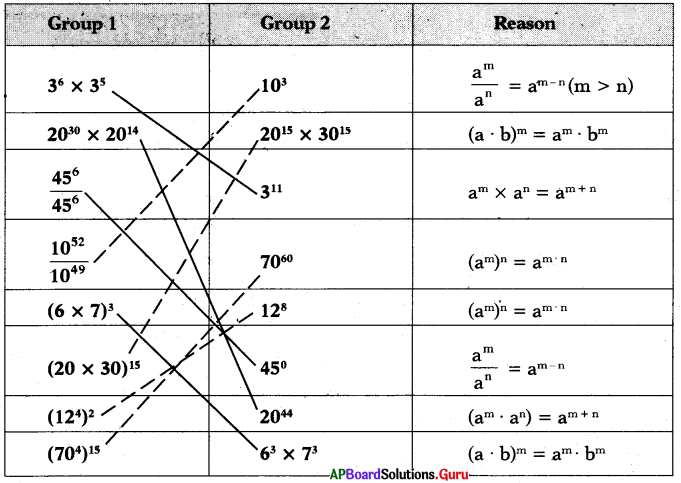
Note : This activity can be extended till all the children in the class are familiarised with the laws of exponents.
Project Work [Page No. 42]
Collect the annual income of 5 families in your location by observing their ration card and rounded into the nearest thousand / Lakh and express in the exponential form. One done for you.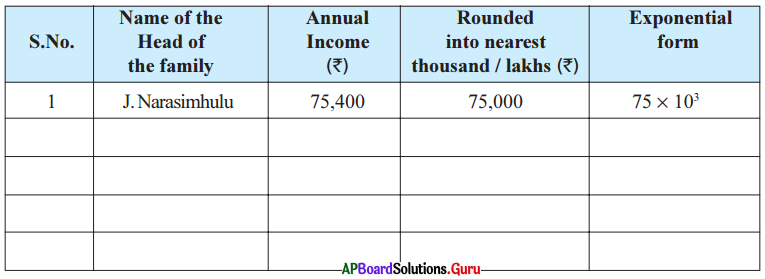
Answer: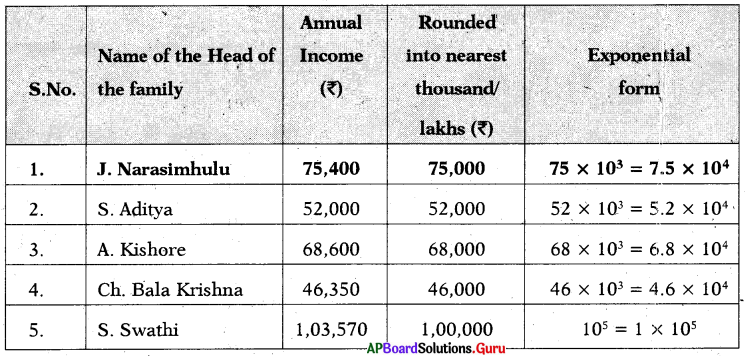
Examples:
Question 1.
Which one is greater 82 or 28? Justify.
Answer:
82 = 8 × 8 = 64
28 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
256 >64
Therefore, 28 > 82.
Question 2.
Simplify the following using the formula am × an = am+n
(i) (- 5)7 × (- 5)4
Answer:
(- 5)7 × (- 5)4 = (- 5)7+4
(∵ am × an = am+n)
= (- 5)11
∴ (- 5)7 × (- 5)4 = (- 5)11
(ii) 33 × 32 × 34
Answer:
33 × 32 × 34 = 33+2+4
(∵ am × an = am+n)
= 39
∴ 33 × 32 × 34 = 39
Question 3.
Simplify the following using the formula (am)n = amn
(i) (83)4
Answer:
(83)4 = 83×4
= 812
∴ (83)4 = 812
(ii) [(-11)5]2
Answer:
[(-11)5]2 = (- 11)5×2
= (- 11)10
∴ [(-11)5]2 = (- 11)10
(iii) (750)2
Answer:
(750)2= 750×2 = 7100
∴ (750)2 = 7100
Question 4.
Simplify the following using the expo-nential law am × bm = (ab)m
(i) 52 × 32
Answer:
52 × 32 = (5 × 3)2 [∵ am × bm = (ab)m]
(ii) p3 × q3
Answer:
p3 × q3 = (p × q)3
(iii) (7 × 8)4
Answer:
(7 × 8)4 = 74 × 84 [∵ (ab)m = am × bm]
Question 5.
Simplify the following and write in the form of 𝑎𝑚𝑎𝑛 = am-n or 𝑎𝑚𝑎𝑛=1𝑎𝑛−𝑚
(i) 2923
Answer:
2923 = 29-3 [∵ 𝑎𝑚𝑎𝑛 = am-n]
= 26
(ii) (−9)11(−9)7
Answer:
(−9)11(−9)7 = (- 9)11-7 = (-9)4
(iii) 710713
Answer:
710713=1713−10
[∵ 𝑎𝑚𝑎𝑛=1𝑎𝑛−𝑚]
= 173
(iv) 6265
Answer:
6265=165−2=163
Question 6.
Simplify the following by using formula 𝑎𝑚𝑏𝑚=(𝑎𝑏)𝑚.
(i) 5323
Answer:
5323=(52)3 [∵ 𝑎𝑚𝑏𝑚=(𝑎𝑏)𝑚]
(ii) (85)4
Answer:
(85)4=8454
[∵ 𝑎𝑚𝑏𝑚=(𝑎𝑏)𝑚]
Question 7.
Evaluate:
(1)4, (1)5, (1)7, (- 1)2, (- 1)3, (- 1)4, (- 1)5
Answer:
(1)4 = 1 × 1 × 1 × 1 = 1
(1)5 = 1 × 1 × 1 × 1 × 1 = 1
(1)7 = 1 × 1 × 1 × 1 × 1 × 1 × 1 = 1
(- 1)2= (-1) × (-1) = 1
(- 1)3 = (-1) × (1) × (-1) = – 1
(- 1)4 =(-1) × (-1) × (-1) × (-1) = 1
(- 1)5 = (-1) × (-1) × (-1) × (-1) × (- 1) = – 1
From the above illustrations,
(i) It raised. to any power is 1.
(ii) (-1) raised to even power is (- 1) and
(-1) raised to an odd power is (-1).
Thus (- 1)m = 1 if ’m’ is even
(- 1)m 1 if ‘m’ is odd
Question 8.
Express In exponential form.
Answer:
-8 = (-2) × (-2) × (-2) = (-2)3
27 = 3 × 3 × 3 = (3)3
∴ −827:(−2)333=(−23)3
Question 9.
Abhllash computed a3. a2 as a6. Is it correct?
Answer:
Abhilash has done it incorrectly.
Bcause a3. a2 = a3+2 = a5 [∵ am . an = amn]
Therefore, a3. a2 = a5 is correct answer.
Question 10.
Riyaz computed 𝑎8𝑎2 as a4. Has he done It correctly? Justify your answer.
Answer:
Riyaz has done it incorrectly.
Because 𝑎8𝑎2 = a8-2
= a6 [∵ 𝑎𝑚𝑎𝑛 = am-n]
∴ 𝑎8𝑎2 = a6 is correct answer.
Question 11.
Write the following into standard form.
(i) 7465
Answer:
7465 = 7.465 × 1000 (Decimal is shifted three places to the left)
= 7.465 × 103
(ii) The height of Mount Everest is 8848 m.
Answer:
The height of Mount Everest
= 8848 m
= 8.848 × 1000 m (Decimal is shifted three places to the left)
= 8.848 × 103m
(iii) The distance from the Sun to Earth is 149,600,000,000 m.
Answer:
The distance from the Sun to Earth
= 149,600,000,000 m
= 1.496 × 100000000000 m
= 1.496 × 1011 m
Reasoning Corner [Page No. 45: Odd one out in numbers]
In each of the following questions, there are 4 numbers. Three of them are similar in a certain way but one is not like the other three. One has to identify the similarity and then strike the odd one out as answer option.
The number can be odd/ even /consecutive, prime numbers, multiple of some number, single, square or cubes of different numbers, plus/minus of some other number or combinations of any mathematical calculation.
Question 1.
(a) 12
(b) 25
(c) 37
(d) 49
Answer:
(c) 37
Hint:
Prime number
Question 2.
(a) 13
(b) 63
(c) 83
(d) 43
Answer:
(b) 63
Hint:
Not a prime number
Question 3.
(a) 21
(b) 49
(c) 56
(d) 36
Answer:
(d) 36
Hint:
Not divisible by 7
Question 4.
(a) 112
(b) 256
(c) 118
(d) 214
Answer:
(b) 256
Hint:
Square number
Question 5.
(a) 42
(b) 21
(c) 84
(d) 35
Answer:
(d) 35
Hint:
Not divisible by 3
Question 6.
(a) 11
(b) 13
(c) 15
(d) 17
Answer:
(c) 15
Hint:
Not a prime number
Question 7.
(a) 10
(b) 11
(c) 15
(d) 16
Answer:
(b) 11
Hint:
Prime number
Question 8.
(a) 49
(b) 63
(c) 77
(d) 81
Answer:
(d) 81
Hint:
Not divisible by 7
Question 9.
(a) 28
(b) 65
(c) 129
(d) 215
Answer:
(a) 28
Hint:
Even number
Question 10.
(a) 51
(b) 144
(c) 64
(d) 121
Answer:
(a) 51
Hint:
Not square number
Practice Questions [Page No. 46]
Question 1.
(a) 3
(b) 9
(c) 5
(d) 7
Answer:
(b) 9
Explanation:
9 is composite number. The remaining numbers are primes.
Question 2.
(a) 6450
(b) 1776
(c) 2392
(d) 3815
Answer:
(d) 3815
Explanation:
All others are even numbers.
Question 3.
(a) 24
(b) 48
(c) 42
(d) 12
Answer:
(c) 42
Explanation:
12, 24 and 48 are multiples of 12.
Question 4.
(a) 616
(b) 252
(c) 311
(d) 707
Answer:
(c) 311
Explanation:
616, 252 and 707 are Palindromes.
Question 5.
(a) 18
(b) 12
(c) 30
(d) 20
Answer:
(d) 20
Explanation:
12, 18 and 30 are 3 (or) 6 multiples. But, 20 is not 3 (or) 6 multiple.
Question 6.
Find the odd one from the given
(a) 3730
(b) 6820
(c) 5568
(d) 4604
Answer:
(a) 3730
Explanation:
3730, All others are divisible by 4.
Question 7.
(a) 2587
(b) 7628
(c) 8726
(d) 2867
Answer:
(a) 2587
Explanation:
All others are formed by 2, 6, 7 and 8.
Question 8.
(a) 63
(b) 29
(c) 27
(d) 25
Answer:
(d) 25
Explanation:
63, 29 and 27 are not squares. 25 only the square.
Question 9.
(a) 23
(b) 37
(c) 21
(d) 31
Answer:
(c) 21
Explanation:
23,37 and 31 are prime numbers.
21 only the composite number.
Question 10.
(a) 18
(b) 9
(c) 21
(d) 7
Answer:
(d) 7
Explanation:
18, 9, 21 are composite numbers.
7 only the prime number.
AP Board Textbook Solutions PDF for Class 7th Maths
- AP Board Class 7
- AP Board Class 7 Maths
- AP Board Class 7 Maths Chapter 1 Integers Review Exercise
- AP Board Class 7 Maths Chapter 1 Integers Ex 1.1
- AP Board Class 7 Maths Chapter 1 Integers Ex 1.2
- AP Board Class 7 Maths Chapter 1 Integers Ex 1.3
- AP Board Class 7 Maths Chapter 1 Integers Ex 1.4
- AP Board Class 7 Maths Chapter 1 Integers Unit Exercise
- AP Board Class 7 Maths Chapter 1 Integers InText Questions
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Review Exercise
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Ex 2.1
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Ex 2.2
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Ex 2.3
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Ex 2.4
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Ex 2.5
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers Unit Exercise
- AP Board Class 7 Maths Chapter 2 Fractions, Decimals and Rational Numbers InText Questions
- AP Board Class 7 Maths Chapter 3 Simple Equations Ex 3.1
- AP Board Class 7 Maths Chapter 3 Simple Equations Ex 3.2
- AP Board Class 7 Maths Chapter 3 Simple Equations Ex 3.3
- AP Board Class 7 Maths Chapter 3 Simple Equations Ex 3.4
- AP Board Class 7 Maths Chapter 3 Simple Equations Unit Exercise
- AP Board Class 7 Maths Chapter 3 Simple Equations InText Questions
- AP Board Class 7 Maths Chapter 4 Lines and Angles Review Exercise
- AP Board Class 7 Maths Chapter 4 Lines and Angles Ex 4.1
- AP Board Class 7 Maths Chapter 4 Lines and Angles Ex 4.2
- AP Board Class 7 Maths Chapter 4 Lines and Angles Ex 4.3
- AP Board Class 7 Maths Chapter 4 Lines and Angles Ex 4.4
- AP Board Class 7 Maths Chapter 4 Lines and Angles Unit Exercise
- AP Board Class 7 Maths Chapter 4 Lines and Angles InText Questions
- AP Board Class 7 Maths Chapter 5 Triangles Review Exercise
- AP Board Class 7 Maths Chapter 5 Triangles Ex 5.1
- AP Board Class 7 Maths Chapter 5 Triangles Ex 5.2
- AP Board Class 7 Maths Chapter 5 Triangles Ex 5.3
- AP Board Class 7 Maths Chapter 5 Triangles Ex 5.4
- AP Board Class 7 Maths Chapter 5 Triangles Ex 5.5
- AP Board Class 7 Maths Chapter 5 Triangles Ex 5.6
- AP Board Class 7 Maths Chapter 5 Triangles Unit Exercise
- AP Board Class 7 Maths Chapter 5 Triangles InText Questions
- AP Board Class 7 Maths Chapter 6 Data Handling Ex 6.1
- AP Board Class 7 Maths Chapter 6 Data Handling Ex 6.2
- AP Board Class 7 Maths Chapter 6 Data Handling Ex 6.3
- AP Board Class 7 Maths Chapter 6 Data Handling Ex 6.4
- AP Board Class 7 Maths Chapter 6 Data Handling Unit Exercise
- AP Board Class 7 Maths Chapter 6 Data Handling InText Questions
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Review Exercise
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.1
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.2
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.3
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.4
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.5
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.6
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Ex 7.7
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion Unit Exercise
- AP Board Class 7 Maths Chapter 7 Ratio and Proportion InText Questions
- AP Board Class 7 Maths Chapter 8 Exponents and Powers Ex 8.1
- AP Board Class 7 Maths Chapter 8 Exponents and Powers Ex 8.2
- AP Board Class 7 Maths Chapter 8 Exponents and Powers Ex 8.3
- AP Board Class 7 Maths Chapter 8 Exponents and Powers Unit Exercise
- AP Board Class 7 Maths Chapter 8 Exponents and Powers InText Questions
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions Review Exercise
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.1
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.2
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.3
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.4
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions Unit Exercise
- AP Board Class 7 Maths Chapter 9 Algebraic Expressions InText Questions
- AP Board Class 7 Maths Chapter 10 Construction of Triangles Review Exercise
- AP Board Class 7 Maths Chapter 10 Construction of Triangles Ex 10.1
- AP Board Class 7 Maths Chapter 10 Construction of Triangles Ex 10.2
- AP Board Class 7 Maths Chapter 10 Construction of Triangles Ex 10.3
- AP Board Class 7 Maths Chapter 10 Construction of Triangles Unit Exercise
- AP Board Class 7 Maths Chapter 10 Construction of Triangles InText Questions
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures Review Exercise
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures Ex 11.1
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures Ex 11.2
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures Ex 11.3
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures Ex 11.4
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures Unit Exercise
- AP Board Class 7 Maths Chapter 11 Area of Plane Figures InText Questions
- AP Board Class 7 Maths Chapter 12 Symmetry Review Exercise
- AP Board Class 7 Maths Chapter 12 Symmetry Ex 12.1
- AP Board Class 7 Maths Chapter 12 Symmetry Ex 12.2
- AP Board Class 7 Maths Chapter 12 Symmetry Ex 12.3
- AP Board Class 7 Maths Chapter 12 Symmetry Ex 12.4
- AP Board Class 7 Maths Chapter 12 Symmetry Unit Exercise
- AP Board Class 7 Maths Chapter 12 Symmetry InText Questions
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు Review Exercise
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు Ex 1.1
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు Ex 1.2
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు Ex 1.3
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు Ex 1.4
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు Unit Exercise
- AP Board Class 7 Maths Chapter 1 పూర్ణ సంఖ్యలు InText Questions
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Review Exercise
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.1
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.2
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.3
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.4
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.5
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు Unit Exercise
- AP Board Class 7 Maths Chapter 2 భిన్నాలు మరియు దశాంశాలు InText Questions
- AP Board Class 7 Maths Chapter 3 సామాన్య సమీకరణాలు Ex 3.1
- AP Board Class 7 Maths Chapter 3 సామాన్య సమీకరణాలు Ex 3.2
- AP Board Class 7 Maths Chapter 3 సామాన్య సమీకరణాలు Ex 3.3
- AP Board Class 7 Maths Chapter 3 సామాన్య సమీకరణాలు Ex 3.4
- AP Board Class 7 Maths Chapter 3 సామాన్య సమీకరణాలు Unit Exercise
- AP Board Class 7 Maths Chapter 3 సామాన్య సమీకరణాలు InText Questions
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు Review Exercise
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు Ex 4.1
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు Ex 4.2
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు Ex 4.3
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు Ex 4.4
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు Unit Exercise
- AP Board Class 7 Maths Chapter 4 రేఖలు మరియు కోణాలు InText Questions
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Review Exercise
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Ex 5.1
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Ex 5.2
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Ex 5.3
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Ex 5.4
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Ex 5.5
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Ex 5.6
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు Unit Exercise
- AP Board Class 7 Maths Chapter 5 త్రిభుజాలు InText Questions
- AP Board Class 7 Maths Chapter 6 దత్తాంశ నిర్వహణ Ex 6.1
- AP Board Class 7 Maths Chapter 6 దత్తాంశ నిర్వహణ Ex 6.2
- AP Board Class 7 Maths Chapter 6 దత్తాంశ నిర్వహణ Ex 6.3
- AP Board Class 7 Maths Chapter 6 దత్తాంశ నిర్వహణ Ex 6.4
- AP Board Class 7 Maths Chapter 6 దత్తాంశ నిర్వహణ Unit Exercise
- AP Board Class 7 Maths Chapter 6 దత్తాంశ నిర్వహణ InText Questions
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Review Exercise
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.1
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.2
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.3
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.4
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.5
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.6
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Ex 7.7
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం Unit Exercise
- AP Board Class 7 Maths Chapter 7 నిష్పత్తి మరియు అనుపాతం InText Questions
- AP Board Class 7 Maths Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు Ex 8.1
- AP Board Class 7 Maths Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు Ex 8.2
- AP Board Class 7 Maths Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు Ex 8.3
- AP Board Class 7 Maths Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు Unit Exercise
- AP Board Class 7 Maths Chapter 8 ఘాతాంకాలు మరియు ఘాతాలు InText Questions
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు Review Exercise
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు Ex 9.1
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు Ex 9.2
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు Ex 9.3
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు Ex 9.4
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు Unit Exercise
- AP Board Class 7 Maths Chapter 9 బీజీయ సమాసాలు InText Questions
- AP Board Class 7 Maths Chapter 10 త్రిభుజాల నిర్మాణం Review Exercise
- AP Board Class 7 Maths Chapter 10 త్రిభుజాల నిర్మాణం Ex 10.1
- AP Board Class 7 Maths Chapter 10 త్రిభుజాల నిర్మాణం Ex 10.2
- AP Board Class 7 Maths Chapter 10 త్రిభుజాల నిర్మాణం Ex 10.3
- AP Board Class 7 Maths Chapter 10 త్రిభుజాల నిర్మాణం Unit Exercise
- AP Board Class 7 Maths Chapter 10 త్రిభుజాల నిర్మాణం InText Questions
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు Review Exercise
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు Ex 11.1
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు Ex 11.2
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు Ex 11.3
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు Ex 11.4
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు Unit Exercise
- AP Board Class 7 Maths Chapter 11 సమతల పటాల వైశాల్యాలు InText Questions
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము Review Exercise
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము Ex 12.1
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము Ex 12.2
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము Ex 12.3
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము Ex 12.4
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము Unit Exercise
- AP Board Class 7 Maths Chapter 12 సౌష్ఠవము InText Questions






0 Comments:
Post a Comment