AP Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

AP Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Book Answers

AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 book solutions pdf online from this page.

Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks Solutions PDF

Andhra Pradesh State Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks. These Andhra Pradesh State Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	7th
Subject	Maths
Chapters	Maths Chapter 9 Algebraic Expressions Ex 9.3
Provider	Hsslive

How to download Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Answers.
Look for your Andhra Pradesh Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions for PDF Free.

AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

Question 1.
Write standard form and additive inverse of the following expressions.
(i) – 6a
Answer:
Additive inverse of – 6a = – (- 6a) = 6a

(ii) 2 + 7c²
Answer:
Standard form of 2 + 7c² = 7c² + 2
Additive inverse of 7c² + 2
= – (7c² + 2)
= – 7c² – 2

(iii) 6x² + 4x – 5
Answer:
Given expression is in standard form.
Additive inverse of 6x² + 4x – 5
= – (6x² + 4x – 5)
= – 6x² – 4x + 5

(iv) 3c + 7a – 9b
Answer:
Standard form of 3c + 7a – 9b = 7a – 9b + 3c
Additive inverse of 7a – 9b + 3c
= – (7a – 9b + 3c)
= – 7a + 9b – 3c

Question 2.
Write the following expressions in standard form:
(i) 6x + x² – 5
Answer:
Standard form of 6x + x² – 5
= x² + 6x – 5

(ii) 3 – 4a² – 5a
Answer:
Standard form of 3 – 4a² – 5a
= – 4a² – 5a + 3

(iii) – m + 6 + 3m²
Answer:
Standard form of – m + 6 + 3m²
= 3m² – m + 6

(iv) c³ + 1 + c + 2c²
Answer:
Standard form of
c³ + 1 + c + 2c² = c³ + 2c² + c + 1

(v) 9 – p²
Answer:
Standard form of 9 – p² = – p² + 9

Question 3.
Add the following algebraic expressions using both horizontal and vertical methods. Did you get the same answer with both the methods? Verify.
(i) 2x² – 6x +3; 4x² + 9x + 5
Answer:

(ii) a² + 6ab + 8; – 3a² – ab – 2
Answer:

(iii) – p² + 2p – 10; 4 – 5p – 2p²
Answer: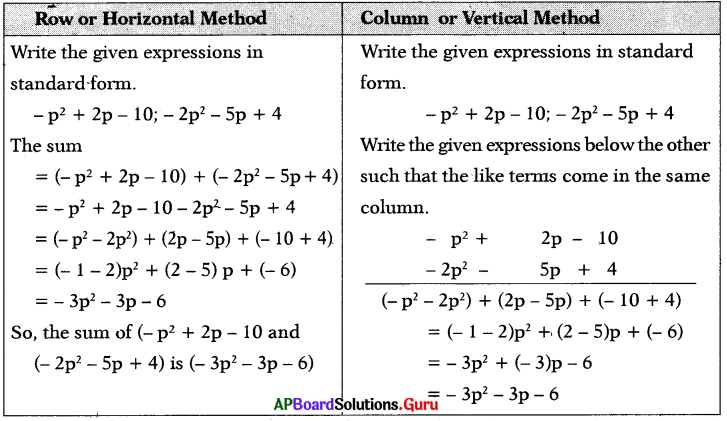

Question 4.
Subtract the second expression from the first expression:
(i) 2x + y , x – y
Answer:
Let A = 2x + y and B = x – y
A – B = A + (- B) Additive inverse of B is
-B = – (x – y) = – x + y
∴ A – B = A + (- B)
= 2x + y + (- x + y)
= 2x + y – x + y
= 2x – x + y + y
= (2 – 1)x + (1 + 1)y
∴ A – B = x + 2y

(ii) a + 2b + c, – a – b – 3c
Answer:
Let A = a + 2b + c and B = – a – b – 3c
A – B = A + (- B)
Additive inverse of B is
– B = – (- a – b – 3c)
= a + b + 3c
∴ A – B = A + (- B)
= a + 2b + c + (a + b + 3c)
= a + 2b + c + a + b + 3c
= (a + a) + (2b + lb) + (c + 3c)
∴ A – B = 2a + 3b + 4c

(iii) 2l² – 3lm + 5m², 3l² – 4lm + 6m²
Answer:
Let A = 2l² – 3lm + 5m² and
B = 3l² – 4lm + 6m²
A – B = A + (- B)
Additive inverse of B is
– B = – (3t² – 4lm + 6m²)
= – 3l² + 4lm – 6m²
∴ A – B = A + (- B)
= (2l² – 3lm + 5m²) + (- 3l² + 4lm – 6m²)
= 2l² – 3lm + 5m² – 3l² + 4lm – 6m²
= 2l² – 3l² – 3lm + 4lm + 5m² – 6m²
= (2 – 3)l² + (- 3 + 4)lm + (5 – 6)m²
= (- 1) l² + 1 lm + (- 1)m²
∴ A – B = – l² + lm – m²

(iv) 7 – x – 3x², 2x² – 5x – 3
Answer:
Let A = 7 – x – 3x² and B = 2x² – 5x – 3
Write the given expressions in standard form.
∴ A = – 3x² – x + 7 and B = 2x² – 5x – 3
A – B = A + (- B)
Additive inverse of B is
– B = – (2x² – 5x – 3)
= – 2x² + 5x + 3
∴ A – B = A + (- B)
= (- 3x² – x + 7) + (- 2x² + 5x + 3)
= – 3x² – x + 7 – 2x² + 5x + 3
= (- 3x² – 2x²) + (- x + 5x) + (7 + 3)
= (- 3 – 2)x² + (- 1 + 5)x + 10
∴ A – B = – 5x² + 4x + 10

(v) 6m³ + 4m² + 7m – 3, 2m³ + 4
Answer:
Let A = 6m³ + 4m² + 7m – 3 and
B = 2 m² + 4
A – B = A + (- B)
Additive inverse of B is
– B = – (2m³ + 4)
= – 2m³ – 4
∴ A – B = A + (- B)
= (6m³ + 4m² + 7m – 3) + (- 2m³ – 4)
= 6m³ + 4m² + 7m – 3 – 2m³ – 4
= (6m³ – 2m³) + 4m² + 7m + (- 3 – 4)
= (6 – 2)m³ + 4m² + 7m + (- 7)
∴ A – B = 4m³ + 4m² + 7m – 7

Question 5.
Find the perimeter of the beside rect¬angle whose length is 6x + y and breadth is 3x – 2y.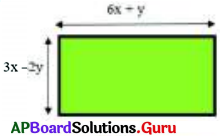

Answer:
Given length of rectangle l = 6x + y
breadth b = 3x – 2y
Perimeter of Rectangle = 2 (l + b)
= 2[(6x + y) + (3x – 2y)]
= 2[6x + y + 3x – 2y]
= 2[(6 + 3)x + (1 – 2)y]
= 2[9x + (- 1) y]
= 2[9x – 1y]
= 2 × (9x) – 2 × (1y)
∴ Perimeter of rectangle = (18x – 2y) units.

Question 6.
Find the perimeter of triangle whose sides are a + 3b, a – b and 2a – b.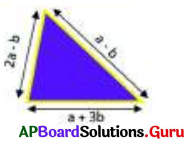

Answer:
Let the sides of triangle are
x = a + 3b, y = a – b and z = 2a – b
Perimeter of triangle = x + y + z
= (a + 3b) + (a – b) + (2a – b)
= a + 3b + a – b + 2a – b
= (a + a + 2a) + (3b – b – b)
= (1 + 1 + 2)a + (3 – 1 – 1)b
Perimeter of triangle.
= (4a + b) units.

Question 7.
Subtract the sum of x² – 5xy + 2y² and y² – 2xy – 3x² from the sum of 6x² – 8xy – y² and 2xy – 2y² – x².
Answer:
Given expressions are
x² – 5xy + 2y² and y² – 2xy – 3x² and 6x² – 8xy – y² and 2xy – 2y² – x²
Write the given expressions in the standard form
x² – 5xy + 2y² and – 3x² – 2xy + y² and 6x² – 8xy – y² and – x² + 2xy – 2y²
Let the Sum
A = (x² – 5xy + 2y²) + (- 3x² – 2xy + y²)
= x² – 5xy + 2y² – 3x² – 2xy + y²
= x² – 3x² – 5xy – 2xy + 2y² + y²
= (1 – 3)x² + (- 5 – 2)xy + (2 + 1)y²
A = – 2x² – 7xy + 3y²

Let the Sum
B = (6x² – 8xy – y²) + (- x² + 2xy – 2y²)
= 6x² – 8xy – y² – x² + 2xy – 2y²
= (6 – 1 )x² + (- 8 + ²)xy + (- 1 – 2)y²
B = 5x² – 6xy – 3y²
B – A = B + (- A)
Additive inverse of A is
– A = – (A)
= – (- 2x² – 7xy + 3y²)
∴ – A = 2x² + 7xy – 3y²
B – A = B + (- A)
= (5x² – 6xy – 3y²) + (2x² + 7xy – 3y²)
= (5 + 2)x² + (- 6 + 7)xy + (- 3 – 3)y²
∴ B – A = 7x² + xy – 6y²

Question 8.
What should be added to 1 + ²p – 3P² to get p² – p – 1 ?
Answer:
Given expressions are
1 + 2p – 3p² and p² – p – 1
Write the given expressions in the standard form.
– 3p² + ²p + 1 and p² – p – 1
Let A should be added to B to get C.
i.e. A + B = C
∴ A = C – B
Let B = – 3p² + 2p + 1 and
C = p² – p – 1
A = C + (- B )
Additive inverse B is
– B = – (- 3p² + 2p + 1) .
– B = 3p² – 2p – 1 .
A = (p² – p – 1) + (3p² – 2p – 1)
= p² – p – 1 + 3p² – 2p – 1
= (1 + 3)p² + (- 1 – 2)p + (- 1 – 1)
∴ A = 4p² – 3p – ²
∴ 4p² – 3p – ² is added to 1 + 2p – 3p² to get p² – p – 1.

Question 9.
What should be taken away from 3a² – 4b² + 5ab + 20 to get – a² – b² + 6ab + 3 ?
Answer:
Given expressions are
3a² – 4b² + 5ab + 20 and – a² – b² + 6ab +3
Let A be taken away from B to get C. that is A = B – C = B + (- C)
Let B = 3a² – 4b² + 5ab + 20 and C = – a² – b² + 6ab + 3 Additive inverse of C is
(- C) = – (- a² – b² + 6ab + 3)
= a² + b² – 6ab – 3
A = B + (- C)
= (3a² – 4b² + 5ab + 20) + (a² + b² – 6ab – 3)
= 3a² – 4b² + 5ab + 20 + a² + b² – 6ab – 3
= 3a² + a² – 4b² + b² + 5ab – 6ab + 20 – 3
= (3 + 1)a² + (- 4 + 1)b² + (5 – 6) ab + (20 – 3)
A = 4a² – 3b² – 1 ab + 17
So, 4a² – 3b² – 1 ab + 17 is taken away from 3a² – 4b² + 5ab + 20 to get – a² – b² + 6ab + 3.

Question 10.
If A = 4x² + y² – 6xy;
B = 3y² + 12x² + 8xy;
C = 6x² + 8y² + 6xy then,
find(i) A + B + C (ii) (A – B) – C
Answer:
Given A = 4x² + y² – 6xy
B = 3y² + 12x² + 8xy
C = 6x² + 8y² + 6xy
Write the given expressions in standard form.
A = 4x² – 6xy + y²
B = 12x² + 8xy + 3y²
C = 6x² + 6xy + 8y²

(i) A + B + C = (4x² – 6xy + y²) + (12x² + 8xy + 3y²) + (6x² + 6xy + 8y²)
= 4x² – 6xy + y² + 12x² + 8xy + 3y² + 6x² + 6xy + 8y²
= (4x² + 12x² + 6x²) + (- 6xy + 8xy + 6xy) + (y² + 3y² + 8y²)
= (4 + 12 + 6) x² + (- 6 + 8 + 6) xy + (1 + 3 + 8)y²
∴ A + B + C = 22x² + 8xy + 12y²

(ii) (A – B) – C
A + (- B) + (- C)
Additive inverse of B is
– B = – (12x² + 8xy + 3y²)
∴ – B = – 12x² – 8xy – 3y²
Additive inverse of C is
– C = -(6x² + 6xy + 8y²)
∴ – C = – 6x² – 6xy – 8y²
A + (- B) + (- C)
= (4x² – 6xy + y²) + (- 12x² – 8xy – 3y²) + (- 6x² – 6xy – 8y²)
= 4x² – 6xy + y² – 12x² – 8xy – 3y² – 6x² – 6xy – 8y²
= (4x² – 12x² – 6x²) + (- 6xy – 8xy – 6xy) + (y² – 3y² – 8y²)
= (4 – 12 – 6)x² + (- 6 – 8 – 6)xy + (1 – 3 – 8)y²
∴ (A – B) – C = – 14x² – 20xy – 10y²

AP Board Textbook Solutions PDF for Class 7th Maths

Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks for Exam Preparations

Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 exam preparation. The AP Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Solutions

How to get AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook Answers??

Students can download the Andhra Pradesh Board Class 7 Maths Chapter 9 Algebraic Expressions Ex 9.3 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3, AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks, Andhra Pradesh State Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3, Andhra Pradesh State Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook solutions, AP Board Class 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks Solutions, Andhra Pradesh Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3, AP Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks, Andhra Pradesh State Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3, Andhra Pradesh State Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbook solutions, AP Board STD 7th Maths Chapter 9 Algebraic Expressions Ex 9.3 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Tuesday, September 20, 2022