AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 1 Real Numbers InText Questions Book Answers

AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 1 Real Numbers InText Questions Book Answers

AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 1 Real Numbers InText Questions books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 1 Real Numbers InText Questions book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 1 Real Numbers InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 1 Real Numbers InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 1 Real Numbers InText Questions Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 1 Real Numbers InText Questions Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 1 Real Numbers InText Questions
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook Solutions Answers PDF Online?

1. Visit our website - Hsslive
2. Click on the Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Answers.
3. Look for your Andhra Pradesh Board STD 10th Maths Chapter 1 Real Numbers InText Questions Textbooks PDF.
4. Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

 

Question 1.
Find q and r for the following pairs of positive integers a and b, satisfying a = bq + r. (Page No. 3)
i) a = 13, b = 3
Answer:
13 = 3 × 4 + 1
here q = 4 ; r = 1

ii) a = 8, b = 80
Answer:
Take a = 80, b = 8
80 = 8 × 10 + 0 here q = 10 ; r = 0

iii) a = 125, b = 5
Answer:
125 = 5 × 25 + 0
here q = 25 ; r = 0

iv) a = 132, b = 11
Answer:
132 = 11 × 12 + 0
here q = 12 ; r = 0

 

Question 2.
Find the HCF of the following by using Euclid division lemma,
i) 50 and 70 (Page No. 4)
Answer:
For given two positive integers a > b;
there exists unique pair of integers q and r satisfying a = bq + r; 0≤r<b.
∴ 70 = 50 × 1 + 20
Here a = 70, b = 50, q = 1, r = 20.
Now consider 50, 20
50 = 20 × 2 + 10
Here a = 50, b = 20, q = 2, r = 10.
Now taking 20 and 10.
20 = 10 × 2 + 0
Here the remainder is zero.
∴ 10 is the HCF of 70 and 50.

 

ii) 96 and 72
Answer:
96 = 72 × 1 + 24
72 = 24 × 3 + 0
∴ HCF = 24

 

iii) 300 and 550
Answer:
550 = 300 × 1 + 250
300 = 250 × 1 + 50
250 = 50 × 5 + 0
∴ HCF = 50

 

iv) 1860 and 2015
Answer:
2015 = 1860 × 1 + 155
1860 = 155 × 12 + 0
∴ HCF = 155

 

Think & Discuss

Question 1.
From the above questions in ‘DO THIS’, what is the nature of q and r? (Page No. 3)
Answer:
Given: a = bq + r
q > 0 and r lies in between 0 and b
i.e. q > 0 and 0 ≤ r < b

 

Question 2.
Can you find the HCF of 1.2 and 0.12? Justify your answer. (Page No. 4)
Answer:
Given: 1.2 and 0.12
we have 1.2 = 1210 = 120100
0.12 = 12100
Now considering the numerators 12 and 120, their HCF is 12.
∴ HCF of 1.2 and 0.12 is 12100 = 0.12
i.e., if x is a factor of y then x is the HCF of x and y.

 

Question 3.
If r = 0, then what is the relationship between a, b and q in a = bq + r of Euclid divison lemma? (Page No. 6)
Answer:
Given: r = 0 in a = bq + r then a = bq
i.e., b divides a completely.
i.e., b is a factor of a.

 

Do this

Question 1.
Express 2310 as a product of prime factors. Also see how your friends have factorized the number. Have they done it as you ? Verify your final product with your friend’s result. Try this for 3 or 4 more numbers. What do you conclude? (Page No. 7)
Answer:
Given: 2310
2310 = 2 × 1155
= 2 × 3 × 385
= 2 × 3 × 5 × 77
2310 = 2 × 3 × 5 × 7 × 11

We notice that this prime factorization is unique.
And also notice that prime factorization of any number is unique i.e., every composite number can be expressed as a product of primes and this factorization is unique.
E.g: 144 = 2 × 72
= 2 × 2 × 36
= 2 × 2 × 2 × 18
= 2 × 2 × 2 × 2 × 9
= 2 × 2 × 2 × 2 × 3 × 3
= 24 × 32
320 = 2 × 160
= 2 × 2 × 80
= 2 × 2 × 2 × 40
= 2 × 2 × 2 × 2 × 20
= 2 × 2 × 2 × 2 × 2 × 10
= 2 × 2 × 2 × 2 × 2 × 2 × 5
= 26 × 5
125 = 5 × 25
= 5 × 5 × 5
= 5³

 

Question 2.
Find the HCF and LCM of the following given pairs of numbers by prime factorization, (Page No. 8)
i) 120, 90
Answer:
We have 120 = 2 × 2 × 2 × 3 × 5
= 2³ × 3 × 5
90 = 2 × 3 × 3 × 5
= 2 × 3² × 5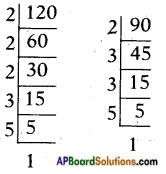

∴ HCF = 2 × 3 × 5 = 30
LCM = 2³ × 3² × 5 = 360

 

ii) 50, 60
Answer:
We have
50 = 2 × 5 × 5 = 2 × 5²
60 = 2 × 2 × 3 × 5 = 2² × 3 × 5

∴ HCF = 2 × 5 = 10
LCM = 2² × 3 × 5² = 300

 

iii) 37, 49
Answer:
We have
37 = 1 × 37
49 = 7 × 7 = 7²
∴ HCF = 1
LCM = 37 × 7²
Note: H.C.F. of two relatively prime numbers is 1 and LCM is equal to product of the numbers.

 

Try this

Question 1.
Show that 3ⁿ × 4^m cannot end with the digit 0 or 5 for any natural numbers ‘n’ and’m’. (Page No. 8)
Answer:
Given number is 3⁴ × 4^m.
So the prime factors to it are 3 and 2 only.
I: but if a number want to be end with zero it should have 2 and 5 as its prime factors, but the given hasn’t ‘5’ as its prime factor.
So it cannot be end with zero.
II : now if a number went to be end with 5 it should have ‘5’ as its one of prime factors. But given 3ⁿ × 4^m do not have 5 as a factor.
So it cannot be end with 5.
Hence proved.

 

Do this

Question 1.
Write the following terminating decimals in the form of p/q, q ≠ 0 and p, q are co-primes.
i) 15.265
ii) 0.1255
iii) 0.4
iv) 23.34
v) 1215.8
What can you conclude about the denominators through this process? (Page No. 10)
Answer:
i) 15.265

ii) 0.1255

iii) 0.4
0.4 = 410 = 25
iv) 23.34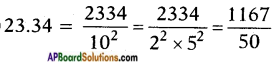

v) 1215.8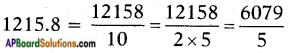

Two and five are the factors for the denominator.

 

Question 2.
Write the following rational numbers in the form of p/q, where q is of the form 2ⁿ.5^m where n, m are non-negative integers and then write the numbers in their decimal form. (Page No. 11)
i) 34
ii) 725
iii) 5164
iv) 1425
v) 80100
Answer:
i) 34
34 = 32×2 = 322

Decimal form of 34 = 0.75

ii) 725
725 = 75×5 = 752

Decimal form of 725 = 0.28

iii) 5164
5164 = 5126
[∵ 64 = 2 × 32
= 2² × 16
= 2³ × 8
= 2⁴ × 4 = 2⁵ × 2 = 2⁶]

Decimal form of 5164 = 0.796875

iv) 1425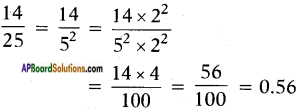

v) 80100
80100 = 8022×52 = 80102 = 0.80

 

Question 3.
Write the following rational numbers as decimal form and find out the block of repeating digits in the quotient. (Page No. 11)
i) 13
ii) 27
iii) 511
iv) 1013
Answer:
i) 13
13 = 0.3333…. = 0.3⎯⎯⎯
Block of digits, repeating in the quotient = period = 3.

ii) 27
Decimal form of 27 = 0.285714….
Repeating part/period = 285714
∴ 27 = 0.285714⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯

iii) 511
Period = 45
Decimal form of 511 = 0.454545.
= 0.45⎯⎯⎯⎯⎯⎯

iv) 1013
Decimal form of 1013 = 0.769230.
= 0.769230⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
Period = 769230

 

Do this

Question 1.
Verify the statement proved above for p = 2, p = 5 and for a² = 1, 4, 9, 25, 36, 49, 64 and 81. (Page No. 14)
Answer: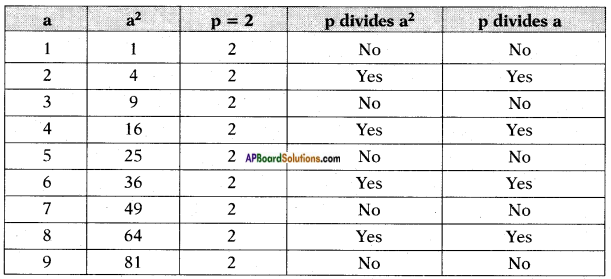


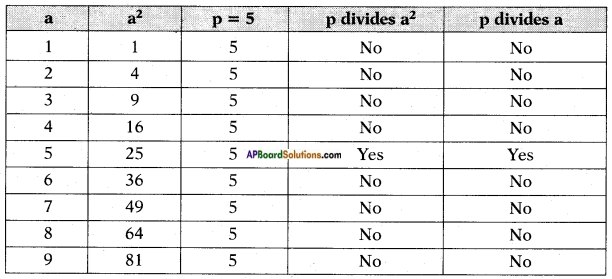
From the above we can conclude that if a prime number ‘p’ divides a², then it also divides a.

 

Think and Discuss

Question 1.
Write the nature of y, a and x in y = a^x. Can you determine the value of x for a given y? Justify your answer. (Page No. 17)
Answer:
y = a^x here a ≠ 0
We can determine the value of ‘x’ for a given y.
for example y = 5, a = 2
We cannot express y = a^x for y = 5, a = 2 and for y = 7, a = 3, we cannot express seven (7) as a power of 3.

 

Question 2.
You know that 2¹ = 2, 4¹ = 4, 8¹ = 8 and 10¹ = 10. What do you notice about the values of log₂ 2, log₄ 4, log₈ 8 and log₁₀ 10? What can you generalise from this? (Page No. 18)
Answer:
From the graph log₂ 2 = log₄ 4 = log₈ 8 = log₁₀ 10 = 1
We conclude that log_a a = 1 where a is a natural number.

 

Question 3.
Does log₁₀ 0 exist? (Page No. 18)
Answer:
No, log₁₀ 0 doesn’t exist, i.e a^x ≠ 0 ∀ a, x ∈ N.

 

Question 4.
We know that, if 7 = 2^x then x = log₂ 7. Then what is the value of 2log27? Justify your answer. Generalise the above by taking some more examples for 𝐚loga𝐍. (Page No. 21)
Answer:
We know that if 7 = 2^x then x = log₂ 7
We want to find the value of 2log27;
Now put log₂ 7 = x in the given
∴ 2log27 = 2^x = 7 (given)
∴ 2log27 = 7
Thus 𝐚loga𝐍 = N

a) 3log38
Answer:
If x = 3log38 then
log₃ x = log₃ 8
⇒ x = 8

b) 5log510
Answer:
If y = 5log510
then log₅ y = log₅ 10
⇒ y = 10

 

Do this

Question 1.
Write the powers to which the bases to be raised in the following. (Page No. 18)
i) 64 = 2^x
Answer:
64 = 2^x
We know that
64 = 2 × 32
= 2 × 2 × 16
= 2 × 2 × 2 × 8
= 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2
64 = 2⁶
⇒ x = 6

ii) 100 = 5^b
Answer:
Here also 100 cannot be written as any power of 5.
i.e., there exists no integer for b such that 5^b = 100

iii) 181 = 3^c
Answer:
We know that 81 = 3 x 27
= 3 × 3 × 9
= 3 × 3 × 3 × 3
= 34
∴ 181 = 3^-4  [∵ a^-m = 1am]
∴ c = – 4

iv) 100 = 10^z
Answer:
100 = 10²
z = 2

v) 1256 = 4^a
Answer:
We know that 256 = 4 × 64
= 4 × 4 × 16
= 4 × 4 × 4 × 4
∴ 1256 = 4^-4
∴ a = – 4

 

Question 2.
Express the logarithms of the following into sum of the logarithms. (Page No. 19)
i) 35 × 46
Answer:
log xy = log x + log y
log₁₀35 × 46 = log₁₀35 + log₁₀46

ii) 235 × 437
Answer:
log₁₀235 × 437 = log₁₀235 + log₁₀437 [∵ log xy = log x + log y]

iii) 2437 × 3568
Answer:
log₁₀ 2437 × 3568 = log₁₀2437 + log₁₀3568 [∵ log xy = log x + log y]

 

Question 3.
Express the logarithms of the follow¬ing into difference of the logarithms. (Page No. 20)
i) 2334
Answer:
log₁₀ = 2334 = log₁₀ 23 – log₁₀ 34
[∵ log 𝑥𝑦 = log x – log y]

ii) 373275
Answer:
log₁₀ = 373275 = log₁₀ 373 – log₁₀ 275
[∵ log 𝑥𝑦 = log x – log y]

iii) 45253734
Answer:
log₁₀ = 45253734 = log₁₀ 4525 – log₁₀ 3734
[∵ log 𝑥𝑦 = log x – log y]

iv) 50553303
Answer:
log₁₀ = 50553303 = log₁₀ 5055 – log₁₀ 3303
[∵ log 𝑥𝑦 = log x – log y]

 

Question 4.
By using the formula log_axⁿ = n log_a x, convert the following. (Page No. 21)
i) log₂ 7²⁵
Answer:
log₂ 7²⁵ = 25 log₂ 7

ii) log₅ 8⁵⁰
Answer:
log₅ 8⁵⁰ = 50 log₅ 8 = 50 log₅ 23
= 3 × 50 log₅2 = 150 log₅2

iii) log 5²³
Answer:
log 5²³ = 23 log 5

iv) log 1024
Answer:
log 1024 = log 2¹⁰ [∵ 1024 = 2¹⁰]
= 10 log 2

 

Try this

Question 1.
Write the following relation in exponential form and find the values of respective variables. (Page No. 18)
i) log₂32 = x
Answer:
log₂32 = x
⇒ log₂2⁵ = x [∵ 32 = 2⁵]
⇒ 5 log₂2 = x [∵ log a^m = m log a]
⇒ 5 × 1 = x [∵ log_a a = 1]
∴ x = 5

ii) log₅625 = y
Answer:
log₅625 = y
⇒ log₅4 = y [∵ 625 = 5⁴]
⇒ 4 log₅ 5 = y [∵ log a^m = m log a]
⇒ 4 × 1 = y [∵ log_a a = 1]
∴ y = 4

iii) log₁₀10000 = z
Answer:
log₁₀10000 = z
=> log₁₀10⁴ = z [∵ 10000 = 10 × 10 × 10 × 10 = 10⁴]
=> 4 log₁₀10 = z [∵ log a^m = m log a]
=> 4 × 1 = z [∵ log_a a = 1]
∴ z = 4

iv) log71343 = -a
Answer:

 

Question 2.
i) Find the value of log₂32. (Page No. 21)
Answer:
log₂ 32 = log₂ 2⁵
[∵ 32 = 2 × 2 × 2 × 2 × 2 = 2⁵]
= 5 log₂ 2 [∵ log a^m = m log a]
= 5 × 1 [∵ log_a a = 1]
= 5

ii) Find the value of log_c √c.
Answer:

= 12 × 1 [∵ log_a a = 1]
= 12

iii) Find the value of log₁₀0.001
Answer: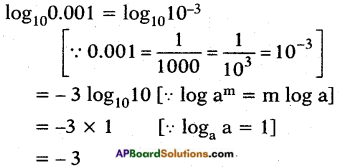

iv) Find the value of log23827
Answer: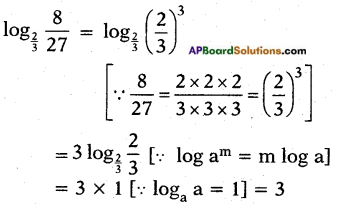

AP Board Textbook Solutions PDF for Class 10th Maths

• AP Board Class 10 10th Textbook Solutions PDF
• AP Board Class 10 Maths Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions exam preparation. The AP Board STD 10th Maths Chapter 1 Real Numbers InText Questions Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 1 Real Numbers InText Questions Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook Solutions

How to get AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 1 Real Numbers InText Questions Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 1 Real Numbers InText Questions, AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 1 Real Numbers InText Questions, Andhra Pradesh State Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbook solutions, AP Board Class 10th Maths Chapter 1 Real Numbers InText Questions Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 1 Real Numbers InText Questions, AP Board STD 10th Maths Chapter 1 Real Numbers InText Questions Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 1 Real Numbers InText Questions, Andhra Pradesh State Board STD 10th Maths Chapter 1 Real Numbers InText Questions Textbook solutions, AP Board STD 10th Maths Chapter 1 Real Numbers InText Questions Textbooks Solutions,