AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Book Answers

AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 9th Lesson Tangents and Secants to a Circle Ex 9.3 Textbook Questions and Answers

Question 1.
A chord of a circle of radius 10 cm. subtends a right angle at the centre. Find the area of the corresponding: (use π = 3.14)
i) Minor segment ii) Major segment
Answer: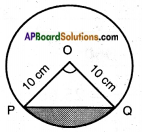

Angle subtended by the chord = 90° Radius of the circle = 10 cm
Area of the minor segment = Area of the sector POQ – Area of △POQ
Area of the sector = 𝑥360 × πr²
90360 × 3.14 × 10 × 10 = 78.5
Area of the triangle = 12 × base × height
= 12 × 10 × 10 = 50
∴ Area of the minor segment = 78.5 – 50 = 28.5 cm²
Area of the major segment = Area of the circle – Area of the minor segment
= 3.14 × 10 × 10 – 28.5
= 314 – 28.5 cm²
= 285.5 cm²

Question 2.
A chord of a circle of radius 12 cm. subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle.
(use π = 3.14 and √3 = 1.732)
Answer:
Radius of the circle r = 12 cm.
Area of the sector = 𝑥360 × πr²
Here, x = 120°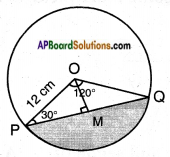

120360 × 3.14 × 12 × 12 = 150.72
Drop a perpendicular from ‘O’ to the chord PQ.
△OPM = △OQM [∵ OP = OQ ∠P = ∠Q; angles opp. to equal sides OP & OQ; ∠OMP = ∠OMQ by A.A.S]
∴ △OPQ = △OPM + △OQM = 2 . △OPM
Area of △OPM = 12 × PM × OM

= 18 × 1.732 = 31.176 cm
∴ △OPQ = 2 × 31.176 = 62.352 cm²
∴ Area of the minor segment
= (Area of the sector) – (Area of the △OPQ)
= 150.72 – 62.352 = 88.368 cm²

Question 3.
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm. sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades. (use π = 227)
Answer:
Angle made by the each blade = 115°
Total area swept by two blades
= Area of the sector with radius 25 cm and angle 115°+ 115° = 230°
= Area of the sector = 𝑥360 × πr²
= 230360 × 227 × 25 × 25
= 1254.96
≃ 1255 cm²

Question 4.
Find the area of the shaded region in figure, where ABCD is a square of side 10 cm. and semicircles are drawn with each side of the square as diameter (use π = 3.14).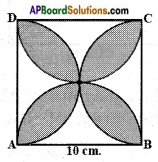

Answer:
Let us mark the four unshaded regions as I, II, III and IV.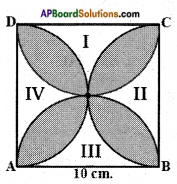

Area of I + Area of II
= Area of ABCD – Areas of two semicircles with radius 5 cm
= 10 × 10 – 2 × 12 × π × 5²
= 100 – 3.14 × 25
= 100 – 78.5 = 21.5 cm²
Similarly, Area of II + Area of IV = 21.5 cm²
So, area of the shaded region = Area of ABCD – Area of unshaded region
= 100 – 2 × 21.5 = 100 – 43 = 57 cm²

Question 5.
Find the area of the shaded region in figure, if ABCD is a square of side 7 cm. and APD and BPC are semicircles. (use π = 227)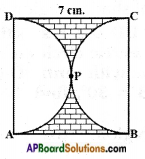

Answer:
Given,
ABCD is a square of side 7 cm.
Area of the shaded region = Area of ABCD – Area of two semicircles with radius 72 = 3.5 cm
APD and BPC are semicircles.
= 7 × 7 – 2 × 12 × 227 × 3.5 × 3.5
= 49 – 38.5
= 10.5 cm²
∴ Area of shaded region = 10.5 cm

Question 6.
In figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm., find the area of the shaded region, (use π = 227).
Answer:
Given, OACB is a quadrant of a Circle.
Radius = 3.5 cm; OD = 2 cm.
Area of the shaded region = Area of the sector – Area of △BOD

= 9.625 – 3.5 = 6.125 cm²
∴ Area of shaded region = 6.125 cm².

Question 7.
AB and CD are respectively arcs of two concentric circles of radii 21 cm. and 7 cm. with centre O (See figure). If ∠AOB = 30°, find the area of the shaded region. (use π = 227).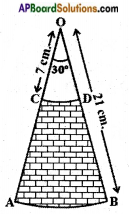

Answer:
Given, AB and CD are the arcs of two concentric circles.
Radii of circles = 21 cm and 7 cm and ∠AOB = 30°
We know that,
Area of the sector = 𝑥360 × πr²
Area of the shaded region = Area of the OAB – Area of OCD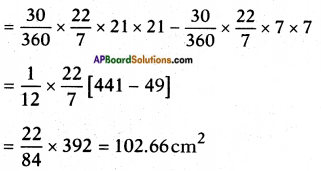

∴ Area of shaded region = 102.66 cm²

Question 8.
Calculate the area of the designed region in figure, common between the two quadrants of the circles of radius 10 cm each, {use π = 3.14)
Answer:
Mark two points P, Q on the either arcs.
Let BD be a diagonal of ABCD
Now the area of the segment

= 28.5 + 28.5 = 57 cm²

Side of the square = 10 cm
Area of the square = side × side
= 10 × 10 = 100 cm²
Area of two sectors with centres A and C and radius 10 cm.
= 2 × 𝜋𝑟2360 × x = 2 × 𝑥360 × 227 × 10 × 10
= 11007
= 157.14 cm²
∴ Designed area is common to both the sectors,
∴ Area of design = Area of both sectors – Area of square
= 157 – 100 = 57 cm²
(or)
11007 – 100 = 1100−7007
= 4007
= 57.1 cm²

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 exam preparation. The AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3, AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3, Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook solutions, AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3, AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3, Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook solutions, AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022