 |
| AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 7 Coordinate Geometry InText Questions Book Answers |
Andhra Pradesh Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbooks Solutions PDF
Andhra Pradesh State Board STD 10th Maths Chapter 7 Coordinate Geometry InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 10th |
| Subject | Maths |
| Chapters | Maths Chapter 7 Coordinate Geometry InText Questions |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Answers.
- Look for your Andhra Pradesh Board STD 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions for PDF Free.
AP Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 10th Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:10th Class Maths 7th Lesson Coordinate Geometry InText Questions and Answers
Do these
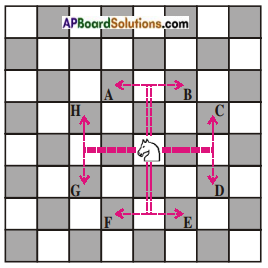
Question 1.
From the figure write coordinates of the points A, B, C, D, E, F, G, H. (Page No. 159)
Answer:
Given: Knight is at the origin (0, 0).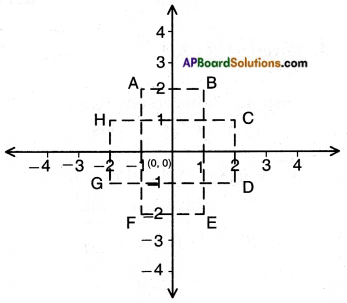
Therefore, A (- 1, 2), B (1, 2), C (2, 1), D (2, – 1), E (1, – 2), F (-1, -2), G (-2, -1) and H (-2, 1).
Question 2.
Find the distance covered by the Knight in each of its 8 moves i.e., find the distance of A, B, C, D, E, F, G and H from the origin. (Page No. 159)
Answer:
Origin (0, 0).
Points A, B, C, D, E, F, G and H.
Distance of any point P(x, y) from the
Question 3.
What is the distance between two points H and C? And also find the distance between two points A and B. (Page No. 159)
Answer:
Given: H (- 2, 1), C (2, 1), A (- 1, 2), B (1, 2).
Distance between any two points P(x1, y1) and Q(x2, y2) is
\(\overline{\mathrm{PQ}}\) = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
∴ Distance between H and C is HC
= \(\sqrt{[2-(-2)]^{2}+(1-1)^{2}}\)
= \(\sqrt{4^{2}+(0)^{2}}\)
= \(\sqrt{16}\)
= 4 units
Distance between A and B is
AB = = \(\sqrt{[1-(-1)]^{2}+(2-2)^{2}}\)
= \(\sqrt{2^{2}+0^{2}}\)
= \(\sqrt{4+0}\)
= 2 units
[!! H, C are points on a line parallel to X – axis.
∴ HC = |x2 – x1| = |2 – (- 2)| = 4 Similarly,
AB = |x2 – x1| = |-1-1| = 2 ]
Question 4.
Where do these following points lie (-4, 0), (2, 0), (6, 0), (-8, 0) on coordinate plane? (Page No. 160)
Answer:
Given points are (- 4, 0), (2, 0), (6, 0), (- 8, 0).
All these points have their y-coordinates = 0
∴ These points lie on X-axis.
Question 5.
What is the distance between points (- 4,0) and (6, 0) on coordinate plane? (Page No. 160)
Answer:
Given points = (- 4, 0) and (6, 0).
These two points lie on the X – axis.
∴ Distance between them = |x2 – x1| = |16 – (-4)| = 16 + 41 = 10 units.
Question 6.
Find the distance between the following pairs of points: (Page No. 162)
i) (3, 8), (6, 8).
Answer:
Given points = A (3, 8) and B (6, 8)
These two points lie on the line parallel to X – axis.
Distance between A (3, 8) and B (6, 8) = |x2 – x1|
= |6 – 3| = 3 units.
ii) (-4, -3), (-8, -3).
Answer:
Given points = A (- 4, – 3) and B (- 8, – 3)
These two points lie on the line parallel to X – axis.
∴ Distance between A (- 4, – 3) and B (- 8, – 3) = |x2 – x1|
= |-8 – (-4)|
= |-8 + 4|
= |-4| = 4 units.
iii) (3, 4), (3, 8).
Answer:
Given points = A (3, 4) and B (3, 8) These two points lie on the line parallel to Y – axis.
∴ Distance between A (3, 4) and B (3, 8)= |y2 – y1|
= |8 – 4| = 4 units.
iv) (-5, -8), (-5, -12).
Answer:
Given points = A (-5, -8) and B (-5, -12)
These two points lie on the line parallel to Y – axis.
∴ Distance between A (-5, -8) and B (-5, -12) = |y2 – y1|
= |-12 – (-8)|
= |-12 + 8|
= |-4| = 4 units.
Question 7.
Find the distance between the following points. (Page No. 162)
i) A = (2, 0) and B(0, 4)
Answer:
Given points = A (2, 0) and B (0, 4)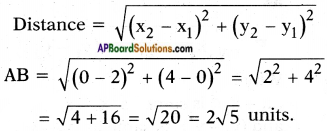
ii) P(0, 5) and Q(12, 0).
Answer:
Given points = P (0, 5) and Q (12, 0)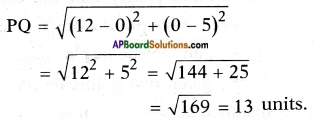
Question 8.
Find the distance between the following pair of points. (Page No. 164)
i) (7, 8) and (- 2, 3)
Answer:
Given points = (7, 8) and (- 2, 3)
Distance formula
ii) (- 8, 6) and (2, 0)
Answer:
Given points = (- 8, 6) and (2, 0).
Distance formula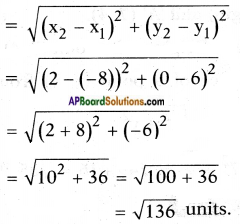
Try these
Question 1.
Where do these following points lie – (0, -3), (0, -8), (0, 6), (0, 4) on coordinate plane? (Page No. 161)
Answer:
As the x – coordinate of all these points is zero, all points lie on Y – axis.
Question 2.
What is the distance between (0, -3), (0, -8) and justify that the distance between two points on Y – axis is |y2 – y1| on coordinate plane? (Page No. 161)
Answer:
As the given two points lie on Y-axis, distance between them is
|y2 – y1| = |-3 + 8| = |5| = 5 units.
Let (0, y1) and (0, y2) be any two points on Y-axis, then distance between them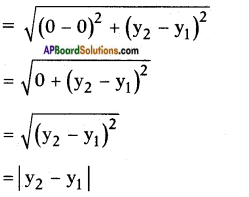
[∵ distance can’t be negative]
Question 3.
Find the distance between points ‘O’(origin) and ‘A’ (7, 4). (Page No. 162)
Answer:
Given: Origin and a point (7, 4).
Distance of a point (x, y) from the origin is \(\sqrt{x^{2}+y^{2}}\)
= \(\sqrt{7^{2}+4^{2}}\) = \(\sqrt{49+16}\) = √65 units.
Question 4.
Find the distance between A(1, -3) and B(-4, 4) and rounded to two decimals. (Page No. 164)
Answer:
Think & Discuss
Question 1.
How will you find the distance between two points in which x or y coordinates are same but not zero? (Page No. 161)
Answer:
Let the points be A(2, 3), B(2, 5).
Here the x-coordinates are same, then the distance between the points A and B is |y2 – y1| = |5 – 3| = 2 units.
If the points are P (4, 3), Q (- 8, 3),
here the y-coordinates are same. In such a case, the distance is given by |x2 – x1| = |-8-4| = |-12|
= 12 units.
i.e.,
Question 2.
Ramu says the distance of a point P(x, y) from the origin O(0, 0) is \(\sqrt{x^{2}+y^{2}}\). Do you agree with Ramu or not? Why? (Page No. 163)
Answer:
Yes. The distance between O(0, 0) and
P(x, y) is \(\sqrt{(x-0)^{2}+(y-0)^{2}}\)
= \(\sqrt{x^{2}+y^{2}}\)
Question 3.
Ramu also writes the distance formula as AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\). Why? (Page No. 163)
Answer:
(x1 – x2)2 is same as (x2 – x1)2
and (y1 – y2)2 is same as (y2 – y1)2
Question 4.
Sridhar calculated the distance between T(5, 2) and R(-4, -1) to the nearest tenth is 9.5 units. Now you find the distance between P (4, 1) and Q (-5, -2). Do you get the same answer that Sridhar got? Why? (Page No. 164)
Answer:
Given points (4, 1), (-5, -2)
We got the same answer.
∵ (x)2 = (-x)2
(x1 – x2)2 = (x2 – x1)2 or
The given points (4, 1) and (-4, -1) are images to each other and (5, 2), (-5, -2) are also images to each other.
Do these
Question 1.
Find the point which divides the line segment joining the points (3, 5) and (8, 10) internally in the ratio 2 : 3. (Page No. 171)
Answer:
Let P (x, y) be the required point then, P (x, y) =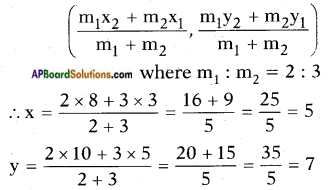
∴ P (x, y) = (5, 7)
Question 2.
Find the midpoint of the line segment joining the points (2, 7) and (12, -7). (Page No. 171)
Answer:
Midpoint of the line joining the points (x1, y1) and (x2, y2) is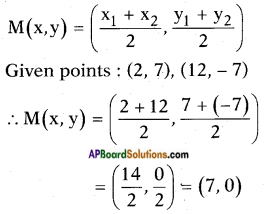
Question 3.
Find the centroid of the triangle whose vertices are (-4, 6), (2, -2) and (2, 5) respectively. (Page No. 173)
Answer:
Given points: (- 4, 6), (2, – 2) and (2,-5).
The coordinates of the centroid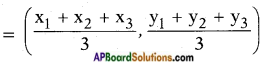
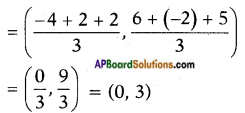
∴ the centroid is (0, 3)
Question 4.
Find the trisectional points of line joining (2, 6) and (-4, 8). (Page No. 175)
Answer:
A (2, 6) and B (- 4, 8) be the given points.
Let P, Q divide the line joining of \(\overline{\mathrm{AB}}\) in the ratio 1 : 2 and 2 : 1.
Section formula (x, y)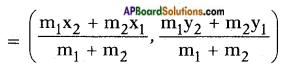
For P(x, y) the ratio is 1 : 2.
P(x,y).
For Q (x, y) the ratio is 2 : 1.
Q (x, y)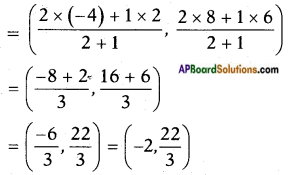
∴ The points of trisection are \(\left(0, \frac{20}{3}\right)\) and \(\left(-2, \frac{22}{3}\right)\).
Question 5.
Find the trisectional points of line joining (-3, -5) and (-6, -8). (Page No. 175)
Answer:
Given: A (- 3, – 5) and B (- 6, 8).
Let P and Q be the points of trisection of \(\overline{\mathrm{AB}}\), then P divides \(\overline{\mathrm{AB}}\) in the ratio 1 : 2.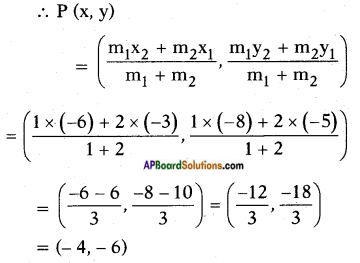
Q (x, y) divides \(\overline{\mathrm{AB}}\) in the ratio 2 : 1
Q (x, y)
∴ The points of trisection are P (-4, -6) and Q (-5, -7).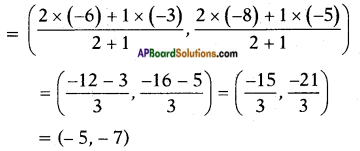
Try these
(Page No. 172)
Let A(4,2), B(6, 5) and C(l, 4) be the vertices of △ABC.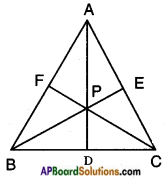
Question 1.
The median from A meets BC at D. Find the coordinates of the point D.
Answer:
D is the midpoint of BC
Question 2.
Find the coordinates of the point P on AD such that AP : PD = 2 : 1. (Page No. 172)
Answer:
P is a point on AD which divides AD in the ratio 2 : 1
∴ P(x,y)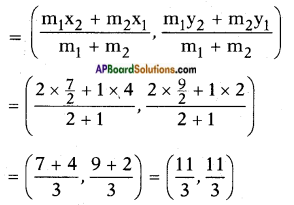
Midpoint of the line joining the points (x1, y1) and (x2, y2) is
Question 3.
Find the points which divide the line segment BE in the ratio 2 : 1 and also that divide the line segment CF in the ratio 2 : 1. (Page No. 172)
Answer:
Given: B (6, 5), E\(\left(\frac{5}{2}, 3\right)\)
Let it be P(x, y) =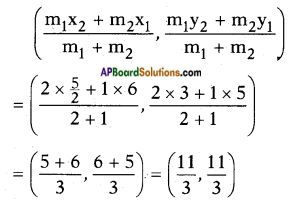
Similarly, let P divide C(1, 4) and F\(\left(5, \frac{7}{2}\right)\) in the ratio 2:1.
Question 4.
What do you observe? Justify the point that divides each median in the ratio 2 : 1 is the centriod of a triangle. (Page No. 172)
Answer:
From the above problems, we conclude that the point ‘P’ divides each median in the ratio 2:1.
i.e., the three medians are concurrent at P, which is called the centroid.
A centriod divides each median in the ratio 2 : 1.
Question 5.
The points (2, 3) (x, y) (3, -2) are the vertices of a triangle. If the centroid of this triangle is origin then find (x, y). (Page No. 173)
Answer:
Given vertices of triangle are (2, 3) (x, y) (3, -2)
now formula for centroid
∴ 5 + x = 0 and 1 + y = 0
⇒ x = -5 and y = -1
∴ (x, y) = (-5, -1)
Think & Discuss
(Page No. 174)
Question 1.
The line joining points A(6, 9) and B(-6, -9) are given.
a. In which ratio does origin divide \(\overline{\mathrm{AB}}\)? And what it is called for \(\overline{\mathrm{AB}}\)?
Answer:
Given : A (6, 9), B (-6, -9)
Let origin O(0, 0) divides \(\overline{\mathrm{AB}}\) in the ratio k : 1 internally.
[By section formula]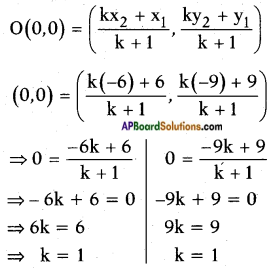
The ratio is 1 : 1.
Here the origin bisects \(\overline{\mathrm{AB}}\).
∴ Origin is called the midpoint of \(\overline{\mathrm{AB}}\).
b. In which ratio does the point P(2, 3) divide \(\overline{\mathrm{AB}}\)?
Answer:
Given: A (6, 9), B (-6, -9) and P (2, 3) divide \(\overline{\mathrm{AB}}\) internally in the ratio say k : 1. [By section formula]
Then P (2, 3) =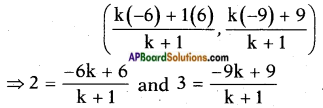
⇒ 2k + 2 = -6k + 6 and 3k + 3 = -9k + 9
⇒ 8k = 6 – 2 and 3k + 9k = 9 – 3
⇒ k = \(\frac{4}{8}\) and 12k = 6
⇒ k = \(\frac{1}{2}\) and k = \(\frac{6}{12}\)
⇒ k = \(\frac{1}{2}\)
∴ The ratio (k : 1) = \(\left(\frac{1}{2}: 1\right)\) = 2 : 1
c. In which ratio does the point Q(-2, -3) divide \(\overline{\mathrm{AB}}\)?
Answer:
Let Q divide \(\overline{\mathrm{AB}}\) in the ratio say k : 1 internally, then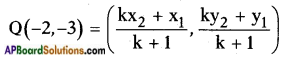
[By section formula]
⇒ 6k + 6 = -2k-2 and -9k + 9 = -3k-3
⇒ -6k + 2k = -2-6 and -9k + 3k = -3-9
⇒ -4k = -8 and -6k = -12
⇒ k = \(\frac{-8}{-4}\) = 2 and k = \(\frac{-12}{-6}\) = 2
∴ The ratio is k : 1 = 2 : 1
d. Into how many equal parts is \(\overline{\mathrm{AB}}\) divided by P and Q?
Answer:
Since P, Q divide \(\overline{\mathrm{AB}}\) in the ratio 1 : 2 and 2 : 1, \(\overline{\mathrm{AB}}\) is divided into three equal parts by P and Q.
e. What do we call P and Q for \(\overline{\mathrm{AB}}\)?
Answer:
P and Q are the points of trisection of \(\overline{\mathrm{AB}}\).
Do these
Question 1.
Find the area of the triangle whose vertices are
(5, 2) (3,-5) and (-5,-1). (Page No. 180)
Answer:
Given: The vertices of the triangle are (5, 2), (3, -5) and (-5, -1).
Area of the triangle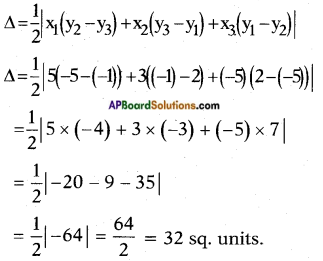
Question 2.
(6, -6), (3, -7) and (3, 3). (Page No. 180)
Answer:
Given: The vertices of a*triangle are (6, -6), (3, -7) and (3, 3).
Area of a triangle
Question 3.
Verify whether the following points are collinear or not. (Page No. 182)
i) (1, -1), (4, 1), (-2, -3).
Answer:
Given: Three points (1, -1), (4, 1), (-2, -3).
Area of the triangle
As the area of the triangle is ‘O’, the three points are collinear.
ii) (1, -1), (2, 3), (2, 0).
Answer:
Given points are (1, -1), (2, 3), (2, 0).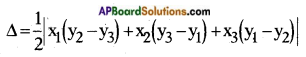
Area of the triangle formed by the given three points is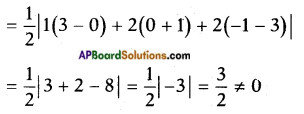
△ ≠ 0.
Hence the points are not collinear.
iii) (1, -6), (3, -4), (4, -3).
Answer:
The given points are (1, -6), (3, -4), (4, -3).
Area of a triangle
Area of the triangle formed by the given three points is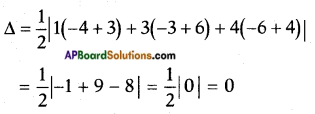
As △ = 0, the points are collinear.
Question 4.
Find the area of the triangle whose lengths of sides are 15 m, 17 m, 21 m. (use Heron’s Formula) (Page No. 183)
Answer:
Given: The sides of a triangle
a = 15 m; b = 17 m and c = 21 m.
Note: As the ‘height’ is not given we can’t verify the above answer by A = \(\frac{1}{2}\)bh
Question 5.
Find the area of the triangle formed by the points (0, 0), (4, 0), (4, 3) by using Heron’s formula. (Page No. 183)
Answer:
The given points are O (0, 0), A (4, 0) and B (4, 3).
Then the sides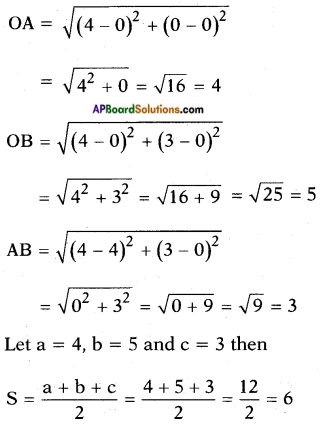
Heron’s formula
Verification:
If the sides are 3, 4 and 5 units, clearly the triangle is a right triangle.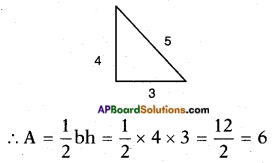
Try these
Question 1.
Take a point A on X-axis and B on Y-axis and find area of the triangle AOB. Discuss with your friends what did they do. (Page No. 178)
Answer: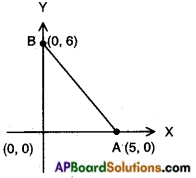
[∴ Axes are perpendicular to each other]
Consider the points A(5, 0) and B(0, 6).
△AOB = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × 6 × 5 = 15 sq. units.
Area of a triangle A (x, 0), O (0, 0) and
B (0, y) is \(\frac{1}{2}\)xy.
Question 2.
Find the area of the square formed by (0, -1), (2, 1), (0, 3) and (-2, 1) taken in order are as vertices. (Page No. 178)
Answer: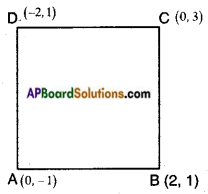
Let A (0, -1), B (2, 1), C (0, 3) and D (- 2, 1) are the vertices of a square.
Area of the square ABCD = side2
= AB2
But, AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-0)^{2}+(1+1)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}\)
= \(\sqrt{4+4}\)
= √8
Area of square = √8 × √8
= 8 sq. units.
Think & Discuss
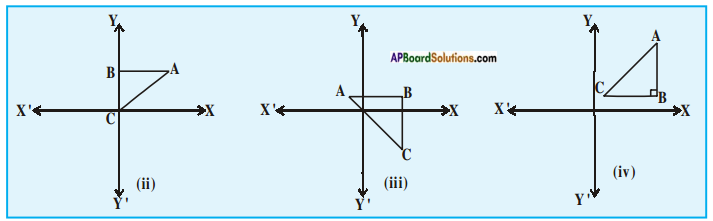
Question 1.
Let A(x1, y1), B(x2, y2), C(x3, y3). Then find the area of the following triangles in a plane. And discuss with your friends in groups about the area of that triangle. (Page No. 178)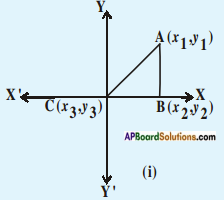
Answer:
i) Given △AOB where A(x1, y1), B(x2, y2) and C(x3, y3)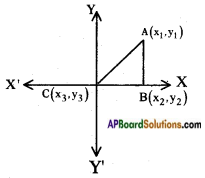
But we know that the origin O is (0, 0) which is given as C.
\(\overline{\mathrm{CB}}\) = x2 – x3 = x2 – 0 = x2
\(\overline{\mathrm{AB}}\) = y1 – y2 = y1 – 0 = y1
∴ Area of △ABC = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\)x2y1
ii)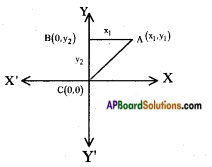
A(x1, y1) = (x1, y1)
B(x2, y2) = (0, y2)
C(x3, y3) = (0, 0)
∴ Area of △ABC = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × y2 × x1
= \(\frac{1}{2}|\)x1y2| sq. units.
iii)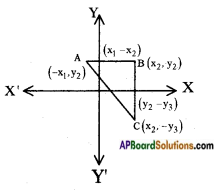
∴ AB = x1 – x2
BC = y2 – y3
A(x1, y1) = (-x1, y1)
B(x2, y2) = (x2, y2)
C(x3, y3) = (x3, -y3)
∴ Area of △ABC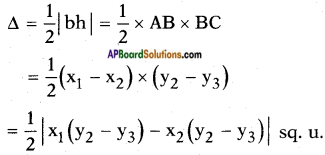
iv)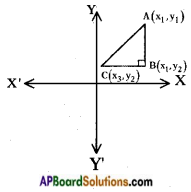
AB = (y2 – y1)
BC = (x1 – x3)
A(x1, y1) = (x1, y1)
B(x2, y2) = (x1, y2)
C(x3, y3) = (x3, y2)
∴ Area of △ABC = \(\frac{1}{2}\) × base × height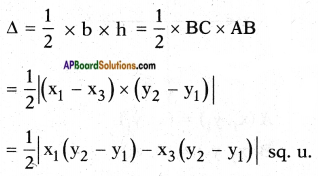
Question 2.
Find the area of the triangle formed by the following points (Page No. 181)
i) (2, 0), (1, 2), (1, 6)
Answer:
Take the third point as (-1, 6).
ii) (3, 1), (5, 0), (1, 2)
Answer:
iii) (-1.5, 3), (6, 2), (-3, 4)
Answer:
Take the second point as (6, -2)
Question 3.
What do you observe? (Page No. 181)
Answer:
We observe that the area formed by above all triangles is zero.
Question 4.
Plot these points on three different graphs. What do you observe? (Page No. 181)
Answer: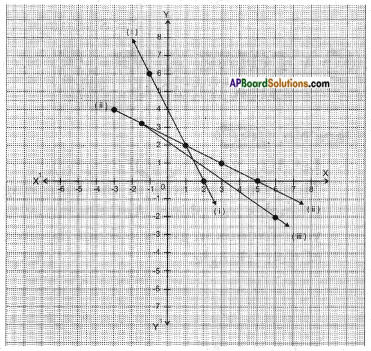
We observe that the points are collinear.
Question 5.
Can we have a triangle having area zero square units area? (Page No. 181)
Answer:
No.
Question 6.
What does it mean? (Page No. 181)
Answer:
If the area of the triangle formed by any three points is zero, it means the points are collinear.
Do these
Question 1.
Plot these points on the coordinate axis and join them:
Which gives a straight line? Which is not? Why? (Page No. 185)
i) A(1, 2), B(-3, 4), C(7, -1)
Answer:
Points ABC gives a straight line.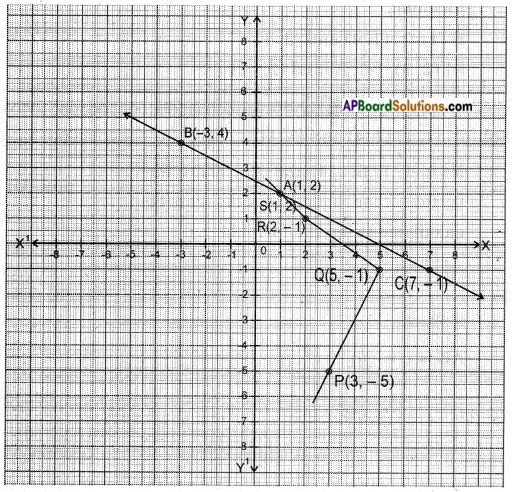
ii) P(3, -5), Q(5, -1), R(2, 1), S(1, 2)
Answer:
Points PQRS doesn’t give a straight line.
Question 2.
Find the slope of \(\overleftrightarrow{\mathbf{A B}}\) with the given end points, (Page No. 188)
i) A(4, -6), B(7, 2)
Answer: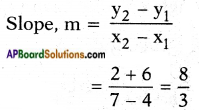
ii) A(8, -4), B(-4, 8)
Answer: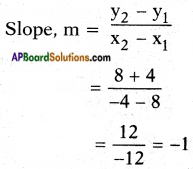
iii) A(-2, -5), B(l, -7)
Answer: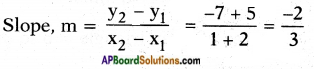
Try these
(Page No. 188)
Question 1.
Find the slope of AB with the points lying on
i) A(2, 1), B(2, 6)
Answer:
Question 2.
A(-4, 2), B(-4, -2)
Answer:
Question 3.
A(-2, 8), B(-2, -2)
Answer:
Question 4.
Justify that the line AB line segment formed by given points is parallel to Y-axis. What can you say about their slope? Why?
Answer:
In the above problem, all points are of the form (K, y) where K is a fixed number and y is a variable.
∴ All lines in the above problem are parallel to Y – axis. Slope of lines parallel to y – axis are not defined.
Think & Discuss
Question 1.
Does y = x + 7 represent a straight line? Draw the line on the coordinate plane. At which point does this line intersect Y – axis?
How much angle does it make with X – axis? Discuss with your friends. (Page No. 185)
Answer:
Yes. y = x + 7 represents a straight line.
Angle made by y = x + 7 with X-axis is 45°. (∵ (0, 7) and (- 7, 0) are equidistant from the origin and hence the triangle formed is right isosceles triangle.)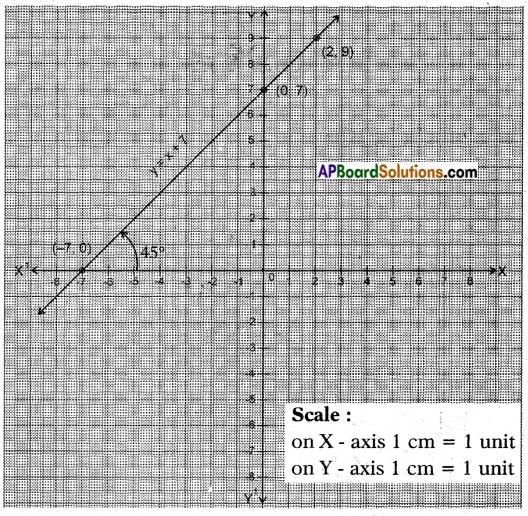
Question 2.
Find the slope AB with the points lying on A(3, 2), B(- 8, 2). When the line AB parallel to X-axis? Why? Think and discuss with your friends in groups. (Page No. 188)
Answer:
Given : A (3, 2), B (-8, 2)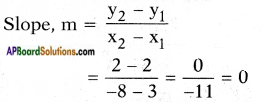
Yes. The line is parallel to X-axis as the points are of the form (x1, K), (x2, K)
AP Board Textbook Solutions PDF for Class 10th Maths
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF






0 Comments:
Post a Comment