Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbooks Solutions PDF
Andhra Pradesh State Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 10th |
| Subject | Maths |
| Chapters | Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Answers.
- Look for your Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions for PDF Free.
AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables Ex 4.3 Textbook Questions and Answers
Question 1.
Solve each of the following pairs of equations by reducing them to a pair of linear equations.
i) 5𝑥−1 + 1𝑦−2 = 2
6𝑥−1 + 3𝑦−2 = 1
Answer:
Given
5𝑥−1 + 1𝑦−2 = 2
6𝑥−1 + 3𝑦−2 = 1
Put 1𝑥−1 = a and 1𝑦−2 = b,
then the given equations reduce to
5a + b = 2 ……… (1)
6a – 3b = 1 ………. (2)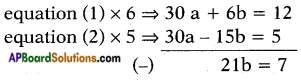
⇒ b = 721 = 13
Substituting b = 13 in equation (1) we get
⇒ (x – 1) . 1 = 3 × 1
⇒ x – 1 = 3
⇒ x = 3 + 1 = 4
b = 1𝑦−2 ⇒ 13 = 1𝑦−2
⇒ (y – 2) . 1 = 3 × 1
⇒ y – 2 = 3
⇒ y = 3 + 2 = 5
∴ Solution (x, y) = (4, 5)
ii) 𝑥+𝑦𝑥𝑦 = 2;
𝑥−𝑦𝑥𝑦 = 6
Answer:
Given
𝑥+𝑦𝑥𝑦 = 2
⇒ 𝑥𝑥𝑦 + 𝑦𝑥𝑦 = 2
⇒ 1𝑦 + 1𝑥 = 2
𝑥−𝑦𝑥𝑦 = 6
⇒ 𝑥𝑥𝑦 – 𝑦𝑥𝑦 = 6
⇒ 1𝑦 – 1𝑥 = 6
Take 1𝑥 = a and 1𝑦 = b,
then the given equations reduces to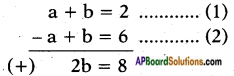
⇒ b = 82 = 4
Substituting b = 4 in equation (1) we get
a + 4 = 2 ⇒ a = 2 – 4 = -2
but a = 1𝑥 = -2 ⇒ x = −12
b = 1𝑦 = 4 ⇒ y = 14
∴ Solution (x, y) = (−12,14)
iii) 2𝑥√ + 3𝑦√ = 2;
4𝑥√ – 9𝑦√ = -1
Answer:
Given
2𝑥√ + 3𝑦√ = 2 and 4𝑥√ – 9𝑦√ = -1
Take 1𝑥√ = a and 1𝑦√ = b,
then the given equations reduces to
2a + 3b = 2 …….. (1)
4a – 9b = – 1 …….. (2)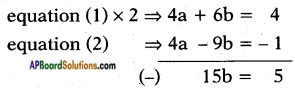
⇒ b = 515 = 13
Substituting b = 13 in equation (1) we get
2a + 3(13) = 2
⇒ 2a + 1 = 2 ⇒ 2a = 2 – 1 ⇒ a = 12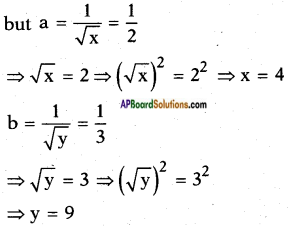
∴ Solution (x, y) = (4, 9)
iv) 6x + 3y = 6xy
2x + 4y = 5xy
Answer:
Given
6x + 3y = 6xy
⇒ 6𝑥+3𝑦𝑥𝑦 = 6
⇒ 6𝑥𝑥𝑦 + 3𝑦𝑥𝑦 = 6
⇒ 6𝑦 + 3𝑥 = 6
2x + 4y = 5xy
⇒ 2𝑥+4𝑦𝑥𝑦 = 5
⇒ 2𝑥𝑥𝑦 + 4𝑦𝑥𝑦 = 6
⇒ 2𝑦 + 4𝑥 = 6
Take 1𝑥 = a and 1𝑦 = b,
then the given equations reduces to
3a + 6b = 6 ……. (1)
4a + 2b = 5 ……. (2)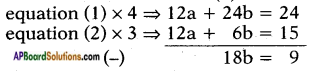
⇒ b = 918 = 12
Substituting b = 12 in equation (1) we get
3a +6(12) = 6
⇒ 3a = 6 – 3
⇒ a = 33 = 1
but a = 1𝑥 = 1 ⇒ x = 1
b = 1𝑦 = 12 ⇒ y = 2
∴ Solution (x, y) = (1, 2)
v) 5𝑥+𝑦 – 2𝑥−𝑦 = -1
15𝑥+𝑦 + 7𝑥−𝑦 = 10
where x ≠ 0, y ≠ 0
Answer:
Given
5𝑥+𝑦 – 2𝑥−𝑦 = -1 and
15𝑥+𝑦 + 7𝑥−𝑦 = 10
Take 1𝑥+𝑦 = a and 1𝑥−𝑦 = b, then
the given equations reduce to
5a – 2b = – 1 ……… (1)
15a + 7b = 10 ……… (2)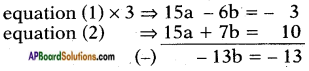
⇒ b = −13−13 = 1
Substituting b = 1 in equation (1) we get
5a – 2(1) = -1
⇒ 5a = -1 + 2
⇒ 5a = 1
⇒ a = 15
but a = 1𝑥+𝑦 = 15 ⇒ x + y = 5
b = 1𝑥−𝑦 = 1 ⇒ x – y = 1
⇒ x = 62 = 3
Solving the above equations
Substituting x = 3 in x + y = 5 we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ Solution (x, y) = (3, 2)
vi) 2𝑥 + 3𝑦 = 13
5𝑥 – 4𝑦 = -2
where x ≠ 0, y ≠ 0
Answer:
Given
2𝑥 + 3𝑦 = 13 and
5𝑥 – 4𝑦 = -2
Take 1𝑥 = a and 1𝑦 = b, then
the given equations reduce to
2a + 3b = 13 ……… (1)
5a – 4b = -2 ……… (2)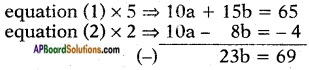
⇒ b = 6923 = 3
Substituting b = 3 in equation (1) we get
2a + 3 (3) = 13
⇒ 2a = 13 – 9
⇒ a = 42 = 2
but a = 1𝑥 = 2 ⇒ x = 12
b = 1𝑦 = 3 ⇒ y = 13
∴ Solution (x, y) = (12, 13)
vii) 10𝑥+𝑦 + 2𝑥−𝑦 = 4
15𝑥+𝑦 – 5𝑥−𝑦 = -2
Answer:
Given
10𝑥+𝑦 + 2𝑥−𝑦 = 4 and
15𝑥+𝑦 – 5𝑥−𝑦 = -2
Take 1𝑥+𝑦 = a and 1𝑥−𝑦 = b, then
the given equations reduce to
10a + 2b = 4 ……… (1)
15a – 5b = – 2 ……… (2)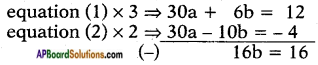
⇒ b = 1616 = 1
Substituting b = 1 in equation (1) we get
10a + 2(1) = 4
⇒ 10a = 4 – 2
⇒ a = 210 = 15
but a = 1𝑥+𝑦 = 15 ⇒ x + y = 5 ……. (3)
b = 1𝑥−𝑦 = 1 ⇒ x – y = 1 …….. (4)
Adding (3) and (4)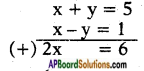
⇒ x = 62 = 3
Substituting x = 3 in x + y = 5 we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ Solution (x, y) = (3, 2)
viii) 13𝑥+𝑦 + 13𝑥−𝑦 = 34
12(3𝑥+𝑦) – 12(3𝑥−𝑦) = −18
Answer:
Given
13𝑥+𝑦 + 13𝑥−𝑦 = 34 and
12(3𝑥+𝑦) – 12(3𝑥−𝑦) = −18
Take 13𝑥+𝑦 = a and 13𝑥−𝑦 = b, then
the given equations reduce to
⇒ a = 28 = 14
Substituting a = 14 in equation (1) we get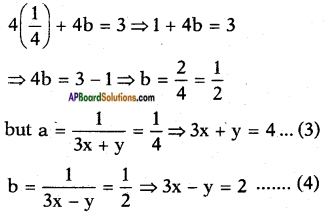
Solving (3) and (4)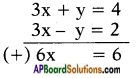
⇒ x = 66 = 1
Substituting x = 1 in 3x + y = 4
⇒ 3(1) + y = 4
⇒ y = 4 – 3 = 1
∴ The solution (x, y) = (1, 1)
Question 2.
Formulate the following problems as a pair of equations and then find their solutions.
i) A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Answer:
Let the speed of the boat in still water = x kmph
and the speed of the stream = y kmph
then speed in downstream = x + y
Speed in upstream = x – y
and time = distance speed
By problem,
30𝑥−𝑦 + 44𝑥+𝑦 = 10
40𝑥−𝑦 + 55𝑥+𝑦 = 13
Take 1𝑥−𝑦 = a and 1𝑥+𝑦 = b, then
the given equations reduce to
30a + 44b = 10 ……… (1)
40a + 55b = 13 ……… (2)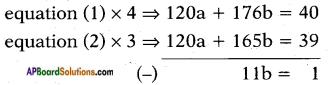
⇒ b = 111
Substituting b = 111 in equation (1) we get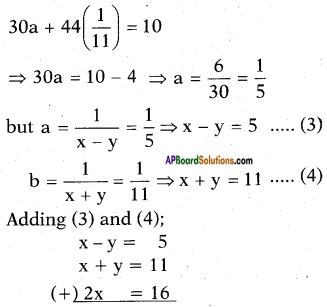
⇒ x = 8
Substituting x = 8 in x – y = 5 we get
8 – y = 5
⇒ y = 8 – 5 = 3
∴ The solution (x, y) = (8, 3)
Speed of the boat in still water = 8 kmph
Speed of the stream = 3 kmph.
ii) Rahim travels 600 km to his home partly by train and partly by car. He takes 8 hours if he travels 120 km by train and rest by car. He takes 20 minutes more if he travels 200 km by train and rest by car. Find the speed of the train and the car.
Answer:
Let the speed of the train be x kmph
and the speed of the car = y kmph
By problem,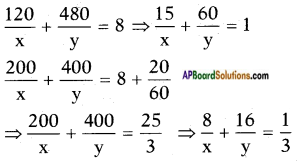
Take 1𝑥 = a and 1𝑦 = b, then
the given equations reduce to
15a + 60b = 1 ……… (1)
8a + 16b = 13 ⇒ 24a + 48b = 1 ……… (2)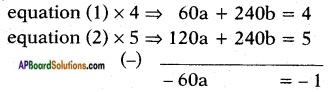
⇒ a = −1−60 = 160
Substituting a = 160 in equation (1) we get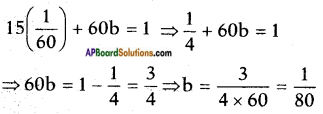
but a = 1𝑥 = 160 ⇒ x = 60 kmph
b = 1𝑦 = 180 ⇒ y = 80 kmph
Speed of the train = 60 kmph and
speed of the car = 80 kmph
iii) 2 women and 5 men can together finish an embroidery work in 4 days while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone and 1 man alone to finish the work.
Answer:
Let the time taken by 1 woman to complete the work = x days
and time taken by 1 man to complete the work = y days
∴ Work done by 1 woman in 1 day = 1𝑥
Work done by 1 man in 1 day = 1𝑦
By problem,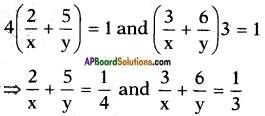
Take 1𝑥 = a and 1𝑦 = b,
then the above equations reduce to
2a + 5b = 14 and 3a + 6b = 13
⇒ 8a + 20b = 1 …….. (1) and
9a + 18b = 1 ……… (2)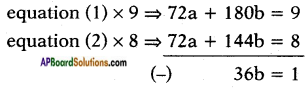
⇒ b = 136
Substituting b = 136 in equation (1) we get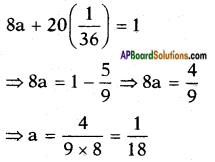
but a = 1𝑥 = 118 ⇒ x = 18 and
b = 1𝑦 = 136 ⇒ y = 36
∴ Time taken by 1 woman = 18 days
1 man = 36 days
AP Board Textbook Solutions PDF for Class 10th Maths
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF







0 Comments:
Post a Comment