AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Book Answers

AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 9th Lesson Tangents and Secants to a Circle Optional Exercise Textbook Questions and Answers

Question 1.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line – segment joining the points of contact at the centre.
Answer: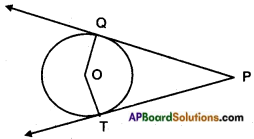

Given: A circle with centre ‘O’.
Two tangents PQ←→ and PT←→ from an external point P. Let Q, T be the points of contact.
R.T.P: ∠P and ∠QOT are supplementary.
Proof: OQ ⊥ PQ
[∵ radius is perpendicular to the tangent at the point of contact] also OT ⊥ PT
∴ ∠OQP + ∠OTP = 90° + 90° = 180° Nowin oPQOT,
∠OTP + ∠TPQ + ∠PQO + ∠QOT
= 360° (angle sum property)
180° + ∠P + ∠QOT = 360°
∠P + ∠QOT = 360°- 180° = 180° Hence proved. (Q.E.D.)

Question 2.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (See figure). Find the length of TP.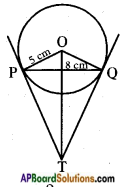

Answer: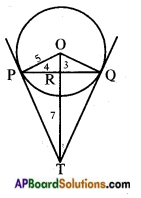

Given: PQ = 8
⇒ PR = 4
⇒ PO² = PR² + OR²
⇒ 25 = 16 + OR²
⇒ OR = 3
Now let RT = x and PT in △OPT, ∠P = 90°
∴ OT is hypotenuse.
∴ OT² = OP² + PT²
(Pythagoras theorem)
(3 + x)² = 5² + y² …….. (1)
and in △PRT, ∠R = 90°
∴ PT⎯⎯⎯⎯⎯⎯⎯ is hypotenuse.
∴ PT² = PR² + RT²
y² = 4² + x² …….. (2)
Now putting the value of y² = 4² + x² in equation (1) we got
(3 + x)² = 5² + x² + 4²
9 + x² + 6x = 25 + 16 + x²
6x = 25 + 16 – 9 = 25 + 7 = 32
⇒ x = 326 = 163
Now from equation (2), we get

Question 3.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer: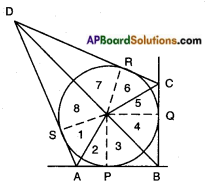

Given: Let a circle with centre ‘O’ touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively.
R.T.P: ∠AOB + ∠COD = 180°
∠AOD + ∠BOC = 180°
Construction: Join OP, OQ, OR and OS.
Proof: Since the two tangents drawn from an external point of a circle subtend equal angles.
At the centre,
∴ ∠1 = ∠2
∠3 = ∠4 (from figure)
∠5 = ∠6
∠7 = ∠8
Now, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
[∵ Sum of all the angles around a point is 360°]
So, 2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
and 2 (∠1 + ∠8 + ∠4 + ∠5) = 360°
(∠2 + ∠3) + (∠6 + ∠7) = 3602 = 180°
Also, (∠1 + ∠8) + (∠4 + ∠5) = 3602 = 180°
So, ∠AOB + ∠COD = 180°
[∵ ∠2 + ∠3 = ∠AOB;
∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD
and ∠4 + ∠5 = ∠BOC [from fig.]]
and ∠AOD + ∠BOC = 180°

Question 4.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Answer: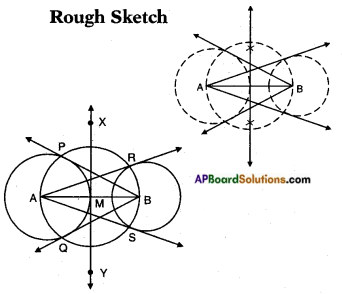

Steps of construction:

Draw a line segment AB of length 8 cm.
With A and B as centres and 4 cm, 3 cm as radius draw two circles.
Draw the perpendicular bisectors XY↔ of AB. Let XY↔ and AB meet at M.
Taking M as centre and MA or MB as radius draw a circle which cuts the circle with centre A at P and Q and circle with centre B at R, S.
Join BP, BQ and AR, AS.

Question 5.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer: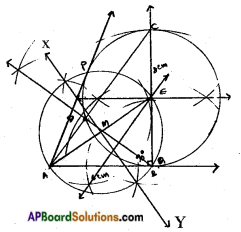

Steps of construction:

Draw AABC such that AB = 6 cm; ∠B = 90° and BC – 8 cm.
Drop a perpendicular BD from B on AC.
Draw the circumcircle to ABCD. Let ‘E’ be its centre.
Join AE and draw its perpendicular bisector XY↔. Let it meet AE at M.
Taking M as centre and MA or ME as radius draw a circle, which’ cuts the circumcircle of △BCD at P and B.
Join AP and extend AB, which are the required tangents.

Question 6.
Find the area of the shaded region in the figure, given in which two circles with centres A and B touch each other at the point C. If AC = 8 cm. and AB = 3 cm.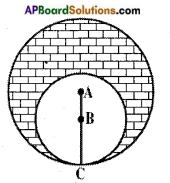

Answer:
Given: Two circles with centres A and B, whose radii are 8 cm and 5 cm.
[∵ AC = 8 cm, AB = 3 cm ⇒ BC = 8 – 3 = 5 cm]
Area of the shaded region = (Area of the larger circle) – (Area of the smaller circle)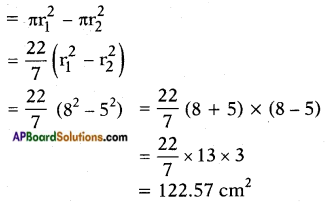

Question 7.
ABCD is a rectangle with AB = 14 cm. and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded region.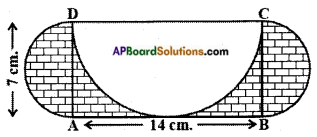

Answer:
Given AB = 14 cm, AD = BC = 7 cm Area of the shaded and unshaded region
= (2 × Area of the semi-circles with AD as diameter) + Area of the rectangle

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise exam preparation. The AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions

How to get AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise, AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise, Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook solutions, AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise, AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise, Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook solutions, AP Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022