AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Book Answers

AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 8 Similar Triangles Ex 8.3
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 8th Lesson Similar Triangles Ex 8.3 Textbook Questions and Answers

Question 1.
Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
Answer: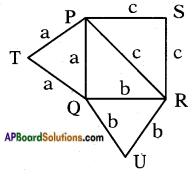

Let △PQR is a right angled triangle, ∠Q = 90°
Let PQ = a, QR b and
PR = hypotenuse = c
Then from Pythagoras theorem we can
say a² + b² = c² ……… (1)
△PSR is an equilateral triangle drawn on hypotenuse
∴ PR = PS = RS = c,
Then area of triangle on hypotenuse
= 3√4c² ……… (2)
△QRU is an equilateral triangle drawn on the side ‘QR’ = b
∴ QR = RU = QU = b
Then area of equilateral triangle drawn on the side = 3√4b² …….. (3)
△PQT is an equilateral triangle drawn on another side ‘PQ’ = a
∴ PQ = PT = QT = a
Area of an equilateral triangle drawn an another side ‘PQ’ = 3√4a² …….. (4)
Now sum of areas of equilateral triangles on the other two sides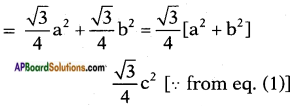

= Area of equilateral triangle on the hypotenuse.
Hence Proved.

Question 2.
Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.
Answer: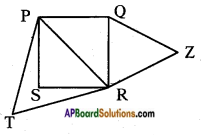

Let PQRS is square whose side is ‘a’ units then PQ = QR = RS = SP = ‘a’ units.
Then the diagonal
PR⎯⎯⎯⎯⎯⎯⎯ = 𝑎2+𝑎2‾‾‾‾‾‾‾√ = a√2 units.
Let △PRT is an equilateral triangle, then PR = RT = PT = a√2
∴ Area of equilateral triangle constructed on diagonal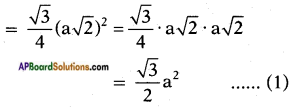

Let △QRZ is another equilateral triangle whose sides are
QR⎯⎯⎯⎯⎯⎯⎯⎯ = RZ⎯⎯⎯⎯⎯⎯⎯⎯ = QZ⎯⎯⎯⎯⎯⎯⎯⎯ = ‘a’ units
Then the area of equilateral triangle constructed on one side of square = 3√4a² ……. (2)
∴ 12 of area of equilateral triangle on diagonal = 12(3√2𝑎2) = 3√4a² = area of equilateral triangle on the side of square.
Hence Proved.

Question 3.
D, E, F are midpoints of sides BC, CA, AB of △ABC. Find the ratio of areas of △DEF and △ABC.
Answer: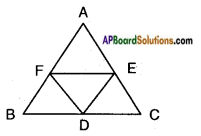

Given in △ABC D, E, F are the midpoints of the sides BC, CA and AB.
In △ABC, EF is the line join of mid-points of two sides AB and AC of △ABC.
Thus FE || BC [∵ 𝐴𝐹𝐹𝐵 = 𝐴𝐸𝐸𝐶 Converse of B.P.T.]
Similarly DE divides AC and BC in the same ratio, i.e., DE || AB.
Now in □ BDEF, both pairs of opposite sides (BD || EF and DE || BF) are parallel.
Hence □ BDEF is a parallelogram where DF is a diagonal.
∴ △BDF ≃ △DEF ……… (1)
Similarly we can prove that
△DEF ≃ △CDE ……… (2)
[∵ CDFE is a parallelogram]
Also, △DEF ≃ △AEF …….. (3)
[∵ □ AEDF is a parallelogram]
From (1), (2) and (3)
△AEF ≃ △DEF ≃ BDF ≃ △CDE
Also, △ABC = △AEF + △DEF + △BDF + △CDE = 4 . △DEF
Hence, △ABC : △DEF = 4 : 1.

Question 4.
In △ABC, XY || AC and XY divides the triangle into two parts of equal area. Find the ratio of 𝐴𝑋𝑋𝐵.
Answer: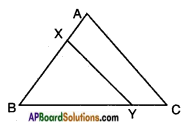

Given: In △ABC, XY || AC.
XY divides △ABC into two points of equal area.
In △ABC, △XBY
∠B = ∠B
∠A = ∠X
∠C = ∠Y
[∵ XY || AC; (∠A, ∠X) and ∠C, ∠Y are the pairs of corresponding angles]
Thus △ABC ~ △XBY by A.A.A similarity condition.
Hence ΔABCΔXBY=AB2XB2
[∵ The ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides]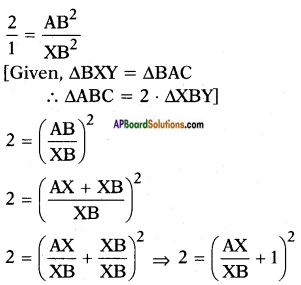

⇒ 𝐴𝑋𝑋𝐵 + 1 = √2
⇒ 𝐴𝑋𝑋𝐵 = √2 – 1
Hence the ratio 𝐴𝑋𝑋𝐵 = √2–11.

Question 5.
Prove that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Answer: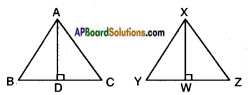

Given: △ABC ~ △XYZ
R.T.P: ΔABCΔXYZ=AD2XW2
Proof : We know that the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Hence the ratio of areas of two similar triangles is equal to the squares of ratio of their corresponding medians.

Question 6.
△ABC ~ △DEF. BC = 3 cm, EF = 4 cm and area of △ABC = 54 cm². Determine the area of △DEF.
Answer: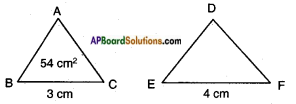

Given: △ABC ~ △DEF
BC = 3 cm
EF = 4 cm
△ABC = 54 cm²
∴ △ABC ~ △DEF, we have
ΔABCΔDEF=BC2EF2
[∵ The ratio of two similar triangles is equal to the ratio of the squares of the corresponding sides].
54ΔDEF = 3242
∴ △DEF = 54×169 = 96 cm²

Question 7.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm and BP = 3 cm, AQ =1.5 cm, CQ = 4.5 cm. Prove that area of △APQ = 116 (area of △ABC).
Answer: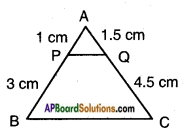

Given: △ABC and PQ⎯⎯⎯⎯⎯⎯⎯⎯ – a line segment meeting AB in P and AC in Q.
AP = 1 cm; AQ =1.5 cm;
BP = 3 cm; CQ = 4.5 cm.
𝐴𝑃𝑃𝑄 = 13 ……… (1)
𝐴𝑄𝑄𝐶 = 1.54.5 = 13 ……..(2)
From (1) and (2),
𝐴𝑃𝐵𝑃 = 𝐴𝑄𝐶𝑄
[i.e., PQ divides AB and AC in the same ratio – By converse of Basic pro-portionality theorem]
Hence, PQ || BC.
Now in △APQ and △ABC
∠A = ∠A (Common)
∠P = ∠B [∵ Corresponding angles for the parallel lines PQ and BC]
∠Q = ∠C
∴ △APQ ~ △ABC [∵ A.A.A similarity condition]
Now, ΔAPQΔABC=AP2AB2
[∵ Ratio of two similar triangles is equal to the ratio of the squares of their corresponding sides].
= 12(3+1)2 = 116 [∵ AB = AP + BP = 1 + 3 = 4 cm]
∴ △APQ = 116 (area of △ABC) [Q.E.D]

Question 8.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. If the altitude of the bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle.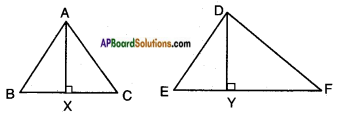

Answer:
Given: △ABC ~ △DEF
△ABC = 81 cm²
△DEF = 49 cm²
AX = 4.5 cm
To find: DY
We know that,
ΔABCΔDEF=AX2DY2
[∵ Ratio of areas of two similar triangles is equal to ratio of the squares of their corresponding altitudes]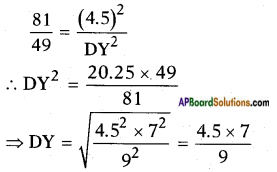

∴ DY = 3.5 cm.

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 exam preparation. The AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3, AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook solutions, AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3, AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbook solutions, AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.3 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022