AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Book Answers

AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Book Answers

AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 8 Similar Triangles Ex 8.4
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions Answers PDF Online?

1. Visit our website - Hsslive
2. Click on the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Answers.
3. Look for your Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks PDF.
4. Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 8th Lesson Similar Triangles Ex 8.4 Textbook Questions and Answers

Question 1.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Answer: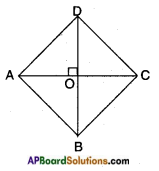

Given : □ ABCD is a rhombus.
Let its diagonals AC and BD bisect each other at ‘O’.
We know that “the diagonals in a rhombus are perpendicular to each other”.
In △AOD; AD² = OA² + OD² ………. (1)
[Pythagoras theorem]
In △COD; CD² = OC² + OD² ………. (2)
[Pythagoras theorem]
In △AOB; AB² = OA² + OB² ………. (3)
[Pythagoras theorem]
In △BOC; BC² = OB² + OC² ………. (4)
[Pythagoras theorem]
Adding the above equations we get AD² + CD² + AB² + BC² = 2 (OA² + OB2 + OC² + OD²)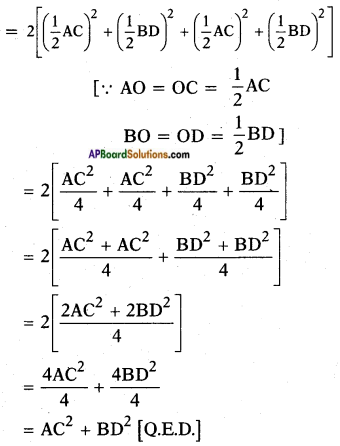

Question 2.
ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively. Prove that AE² + CD² = AC² + DE².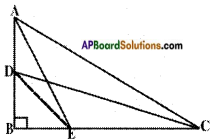

Answer:
Given: In △ABC; ∠B = 90°
D and E are points on AB and BC.
R.T.P.: AE² + CD² = AC² + DE²
Proof: In △BCD, △BCD is a right triangle right angled at B.
∴ BD² + BC² = CD² ……… (1)
[∵ Pythagoras theorem states that hypotenuse² = side² + side²]
In △ABE; ∠B = 90°
Adding (1) and (2), we get
BD² + BC² + AB² + BE² – CD² + AE²
(BD² + BE²) + (AB² + BC²) = CD² + AE²
DE² + AC² – CD² + AE² [Q.E.D.]
[∵ (i) In △DBE, ∠B = 90° and DE² = BD² + BE²
(ii) In △ABC, ∠B = 90° and AB² + BC²]

Question 3.
Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude.
Answer:
Given: △ABC, an equilateral triangle;
AD – altitude and the side is a units, altitude h units.
R.T.P: 3a² = 4h²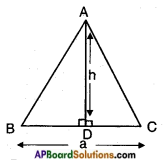

Proof: In △ABD, △ACD
∠B = ∠C [∵ 60°]
∠ADB = ∠ADC [∵ 90°]
∴ ∠BAD = ∠DAC [∵ Angle sum property]
Also, BA = CA
∴ △ABD s △ACD (by SAS congruence condition)
Hence, BD = CD = 12BC = 𝑎2 [∵ c.p.c.t]
Now in △ABD, AB² = AD² + BD²
[∵ Pythagoras theorem]
a² = h² + (𝑎2)2
a² = h² + 𝑎24
h² = 4𝑎2−𝑎24
∴ h² = 3𝑎24
⇒ 4h² = 3a² (Q.E.D)

Question 4.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM . MR.
Answer: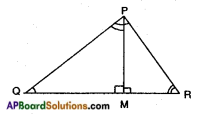

Given: In △PQR, ∠P = 90° and PM ⊥ QR.
R.T.P : PM² = QM . MR
Proof: In △PQR; △MPR
∠P = ∠M [each 90°]
∠R = ∠R [common]
∴ △PQR ~ △MPR ……… (1)
[A.A. similarity]
In △PQR and △MQP,
∠P = ∠M (each 90°)
∠Q = ∠Q (common)
∴ △PQR ~ △MQP ……… (2)
[A.A. similarity]
From (1) and (2),
△PQR ~ △MPR ~ △MQP [transitive property]
∴ △MPR ~ △MQP
𝑀𝑃𝑀𝑄 = 𝑃𝑅𝑄𝑃 = 𝑀𝑅𝑀𝑃
[Ratio of corresponding sides of similar triangles are equal]
𝑃𝑀𝑄𝑀 = 𝑀𝑅𝑃𝑀
PM . PM = MR . QM
PM² = QM . MR [Q.E.D]

Question 5.
ABD is a triangle right angled at A and AC ⊥ BD.
Show that (i) AB² = BC BD
(ii) AD² = BD CD
(iii) AC² = BC DC.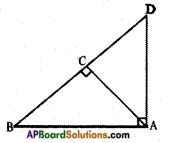

Answer:
Given: In △ABD; ∠A = 90° AC ⊥ BD
R.T.P.:
i) AB² = BC . BD
Proof: In △ABD and △CAB,
∠BAD = ∠ACB [each 90°]
∠B = ∠B [common]
∴ △ABD ~ △CBA
[by A.A. similarity condition]
Hence, 𝐴𝐵𝐵𝐶 = 𝐵𝐷𝐴𝐵 = 𝐴𝐷𝐴𝐶
[∵ Ratios of corresponding sides of similar triangles are equal]
𝐴𝐵𝐵𝐷 = 𝐵𝐶𝐴𝐵
⇒ AB . AB = BC . BD
∴ AB² = BC . BD

ii) AD² = BD . CD
Proof: In △ABD and △CAD
∠BAD = ∠ACD [each 90°]
∠D = ∠D (common)
∴ △ABD ~ △CAD [A.A similarity]
Hence, 𝐴𝐵𝐴𝐶 = 𝐵𝐷𝐴𝐷 = 𝐴𝐷𝐶𝐷
⇒ 𝐵𝐷𝐴𝐷 = 𝐴𝐷𝐶𝐷
AD . AD = BD . CD
AD² = BD . CD [Q.E.D]

iii) AC² = BC . DC
Proof: From (i) and (ii)
△ACB ~ △DCA
[∵ △BAD ~ △BCA ~ △ACD
Hence, 𝐴𝐶𝐷𝐶 = 𝐵𝐶𝐴𝐶 = 𝐴𝐵𝐴𝐷
𝐴𝐶𝐷𝐶 = 𝐵𝐶𝐴𝐶
AC . AC = BC . DC
AC² = BC . DC [Q.E.D]

Question 6.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Answer: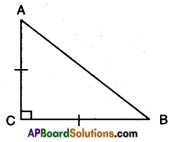

Given: In △ABC; ∠C = 90°; AC = BC.
R.T.P.: AB² = 2AC²
Proof: In △ACB; ∠C = 90°
Hence, AC² + BC² = AB²
[Square of the hypotenuse is equal to sum of the squares of the other two sides – Pythagoras theorem]
⇒ AC² + AC² = AB² [∵ AC = BC given]
⇒ AB² = 2AC² [Q.E.D.]

Question 7.
‘O’ is any point in the interior of a triangle ABC.
OD ⊥ BC, OE ⊥ AC and OF ⊥ AB, show that
i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
ii) AF² + BD² + CE² = AE² + CD² + BF².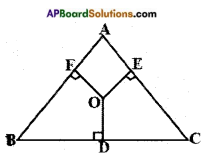

Answer:
Given: △ABC; O’ is an interior point of △ABC.
OD ⊥ BC, OE ⊥ AC, OF ⊥ AB.
R.T.P.:
i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
Proof: In OAF, OA² = AF² + OF² [Pythagoras theorem]
⇒ OA² – OF² = AF² …….. (1)
In △OBD,
OB² = BD² + OD²
⇒ OB² – OD² = BD² …….. (2)
In △OCE, OC² = CE² + OE²
OC² – OE² = CE² ……… (3)
Adding (1), (2) and (3) we get,
OA² – OF² + OB² – OD² + OC² – OE² = AF² + BD² + CE²
OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE² ……… (4)

ii) AF² + BD² + CE² = AE² + CD² + BF²
In △OAE,
OA² = AE² + OF² ……… (1)
⇒ OA² – OE² = AE²
In △OBF, OB² = BF² + OF²
OB² – OF² = BF² ……… (2)
In △OCD, OC² = OD² + CD²
OC² – OD² = CD² ……… (3)
Adding (1), (2) and (3) we get
OA² – OE² + OB² – OF² + OC² – OD² = AE² + BF² + CD²
⇒ OA² + OB² + OC² – OD² – OE² – OF² = AE² + CD² + BF²
⇒ AF² + BD² + CE² = AE² + CD² + BF² [From problem (i)]

Question 8.
A wire attached to vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Answer: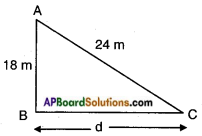

Height of the pole AB = 18 m.
Length of the wire AC = 24 m.
Distance beween the pole and the stake be ‘d’ meters.
By Pythagoras theorem,
Hypotenuse² = side² + side²
24² = 18² + d²
d² = 24² – 18² = 576 – 324 = 252
= 36×7‾‾‾‾‾‾√
∴ d = 6√7 m.

Question 9.
Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Answer: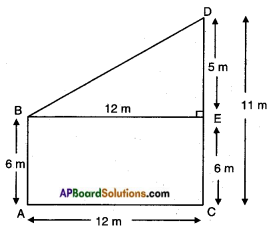

Let the height of the first pole AB = 6 m.
Let the height of the second pole CD = 11 m.
Distance between the poles AC = 12 m.
From the figure □ ACEB is a rectangle.
∴ AB = CE = 6 m
ED = CD – CE = 11 – 6 = 5 m
Now in △BED; ∠E = 90°; DE = 5 m; BE = 12 m
BD² = BE² + DE²
[hypotenuse² = side² + side² – Pythagoras theorem]
= 12² + 5²
= 144 + 25
BD² = 169
BD = √l69 = 13m
∴ Distance between the tops of the poles = 13 m.

Question 10.
In an equilateral triangle ABC, D is a point on side BC such that BD = 13 BC. Prove that 9AD² = 7AB².
Answer: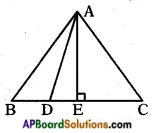

In △ABE, ∠E = 90°
⇒ AB⎯⎯⎯⎯⎯⎯⎯⎯ is hypotenuse.
∴ AB² = AE² + BE²
AE² = AB² – BE²
⇒ AE² = AB² – (𝐵𝐶2)2
= AE² = AB² – (𝐴𝐵2)2 (∵ AB = BC)
⇒ AE² = 34AB² ……… (1)
In △ADE, ∠E = 90°
⇒ AD⎯⎯⎯⎯⎯⎯⎯⎯⎯ is hypotenuse.
⇒ AD² = AE² + DE²
⇒ AE² = AD² + DE²

⇒ 28 AB² = 36 AD²
⇒ 7 AB² = 9 AD²
Hence proved.

Question 11.
In the given figure, ABC is a triangle right angled at B. D and E are points on BC trisect it. Prove that 8 AE² = 3 AC² + 5 AD².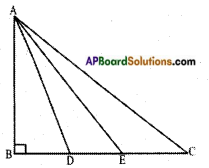

Answer:
In △ABC, ∠B=90°
⇒ AD⎯⎯⎯⎯⎯⎯⎯⎯⎯ is hypotenuse.
AC2 = AB2 + BC2
3AC² = 3AB² + 3BC² …….. (1)
In △ABD, ∠B = 90°
⇒ AD is hypotenuse.
∴ AD² = AB² + BD² = AB² + (𝐵𝐶3)2
⇒ AD² = AB² + BC29
⇒ 5 AD² = 5 AB² + 5BC29 …….. (2)
(1) + (2)
3 AC² + 5 AD² = 3 AB² + 3 BC² + 5 AB² + 59BC2
= 8AB² + 329BC2 ……… (3)
Now in △ABE, ∠B = 90°
⇒ AE⎯⎯⎯⎯⎯⎯⎯⎯ is hypotenuse.
⇒ AE² = AB² + BE² = AB² + (23𝐵𝐶)2
= AB² + 49BC2
⇒ AE² = 8AB² + 329BC2 ……… (4)
∴ RHS of (3) and (4) are equal.
∴ LHS of (3) and (4) are equal.
∴ 8 AE² = 3 AC² + 5 AD².
Hence proved.

Question 12.
ABC is an isosceles triangle right angled at B. Equilateral triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of △ABE and △ACD.
Answer: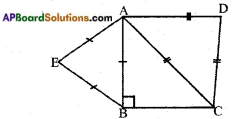

Given: △ABC, AB = BC and ∠B = 90°
△ABE on AB; △ACD on AC are equiangular triangles.
Let equal sides of the isosceles right triangle, AB = BC = a (say)
Then, in △ABC, ∠B = 90°
AC² – AB² + BC²
[hypotenuse² = side² + side² – Pythagoras theorem] = a² + a² = 2a²
Since, △ABE ~ △ACD
ΔABEΔACD = AB2AC2
[∵ Ratio of areas of two similar tri-angles is equal to the ratio of squares of their corresponding sides]
= 𝑎22𝑎2 = 12
△ABE : △ACD = 1 : 2.

AP Board Textbook Solutions PDF for Class 10th Maths

• AP Board Class 10 10th Textbook Solutions PDF
• AP Board Class 10 Maths Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 exam preparation. The AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4, AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook solutions, AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4, AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbook solutions, AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.4 Textbooks Solutions,