Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbooks Solutions PDF
Andhra Pradesh State Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 10th |
| Subject | Maths |
| Chapters | Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Answers.
- Look for your Andhra Pradesh Board STD 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions for PDF Free.
AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 10th Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:10th Class Maths 9th Lesson Tangents and Secants to a Circle Ex 9.2 Textbook Questions and Answers
Question 1.
Choose the correct answer and give justification for each.
(i) The angle between a tangent to a circle and the radius drawn at the point of contact is
a) 60°
b) 30°
c) 45°
d) 90°
Answer: [ d ]
If radius is not perpendicular to the tangent, the tangent must be a secant i.e., 90°.
(ii) From a point Q, the length of the tangent to a circle is 24 cm. and the distance of Q from the centre is 25 cm. The radius of the circle is
a) 7 cm
b) 12 cm
c) 15 cm
d) 24.5 cm
Answer: [ a ]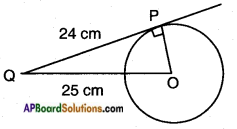
O – centre of the circle
OP – a circle radius = ?
OQ = 25 cm
PQ = 24 cm
OQ2 = OP2 + PQ2
[∵ hypotenuse2 = Adj. side2 + Opp. side2]
252 = OP2 + 242
OP2 = 625 – 576
OP2 = 49
OP = √49 = 7 cm.
iii) If AP and AQ are the two tangents a circle with centre O, so that ∠POQ = 110°. Then ∠PAQ is equal to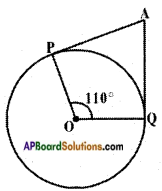
a) 60°
b) 70°
c) 80°
d) 90°
Answer: [ b ]
In □ OPAQ,
∠OPA = ∠OQA = 90°
∠POQ = 110°
∴ ∠O + ∠P + ∠A + ∠Q = 360°
⇒ 90° + 90° + 110° + ∠PAQ – 360°
⇒ ∠PAQ = 360° – 290° = 70°
iv) If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
a) 50°
b) 60°
c) 70°
d) 80°
Answer: [None]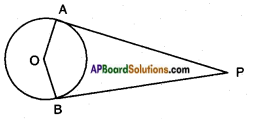
If ∠APB = 80°
then ∠AOB = 180° – 80° = 100°
[∴ ∠A + ∠B = 90° + 90° = 180°]
v) In the figure XY and XV are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and XV at B then ∠AOB =
a) 80°
b) 100°
c) 90°
d) 60°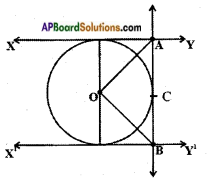
Answer: [ c ]
Question 2.
Two concentric circles of radii 5 cm and 3 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
Given: Two circles of radii 3 cm and 5 cm with common centre.
Let AB be a tangent to the inner/small circle and chord to the larger circle.
Let ‘P’ be the point of contact.
Construction: Join OP and OB.
In △OPB ;
∠OPB = 90°
[radius is perpendicular to the tangent]
OP = 3cm OB = 5 cm
Now, OB2 = OP2 + PB2
[hypotenuse2 = Adj. side2 + Opp. side2, Pythagoras theorem]
52 = 32 + PB2
PB2 = 25 – 9 = 16
∴ PB = √l6 = 4cm.
Now, AB = 2 × PB
[∵ The perpendicular drawn from the centre of the circle to a chord, bisects it]
AB = 2 × 4 = 8 cm.
∴ The length of the chord of the larger circle which touches the smaller circle is 8 cm.
Question 3.
Prove that the parallelogram circumscribing a circle is a rhombus.
Answer: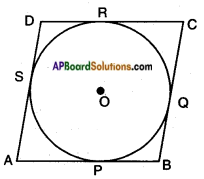
Given: A circle with centre ‘O’.
A parallelogram ABCD, circumscribing the given circle.
Let P, Q, R, S be the points of contact.
Required to prove: □ ABCD is a rhombus.
Proof: AP = AS …….. (1)
[∵ tangents drawn from an external point to a circle are equal]
BP = BQ ……. (2)
CR = CQ ……. (3)
DR = DS ……. (4)
Adding (1), (2), (3) and (4) we get
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + DC = AD + BC
AB + AB = AD + AD
[∵ Opposite sides of a parallelogram are equal]
2AB = 2AD
AB = AD
Hence, AB = CD and AD = BC [∵ Opposite sides of a parallelogram]
∴ AB = BC = CD = AD
Thus □ ABCD is a rhombus (Q.E.D.)
Question 4.
A triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BD and DC into which BC is divided by the point of contact D are of length 9 cm. and 3 cm. respectively (See below figure). Find the sides AB and AC.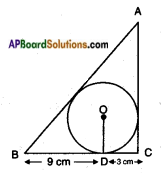
Answer:
The given figure can also be drawn as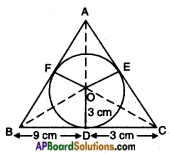
Given: Let △ABC be the given triangle circumscribing the given circle with centre ‘O’ and radius 3 cm.
i.e., the circle touches the sides BC, CA and AB at D, E, F respectively.
It is given that BD = 9 cm
CD = 3 cm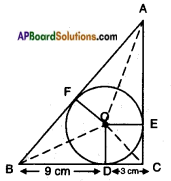
∵ Lengths of two tangents drawn from an external point to a circle are equal.
∴ BF = BD = 9 cm
CD = CE = 3 cm
AF = AE = x cm say
∴ The sides of die triangle are
12 cm, (9 + x) cm, (3 + x) cm
Perimeter = 2S = 12 + 9 + x + 3 + x
⇒ 2S = 24 + 2x
or S = 12 + x
S – a = 12 + x – 12 = x
S – b = 12 + x – 3 – x = 9
S – c = 12 + x – 9 – x = 3
∴ Area of the triangle
Squaring on both sides we get,
27 (x2 + 12x) = (36 + 3x)2
27x2 + 324x = 1296 + 9x2 + 216x
⇒ 18x2 + 108x- 1296 = 0
⇒ x2 + 6x – 72 = 0
⇒ x2 + 12x – 6x – 72 = 0
⇒ x (x + 12) – 6 (x + 12) = 0
⇒ (x – 6) (x + 12) = 0
⇒ x = 6 or – 12
But ‘x’ can’t be negative hence, x = 6
∴ AB = 9 + 6 = 15 cm
AC = 3 + 6 = 9 cm.
Question 5.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Verify by using Pythagoras Theorem.
Answer:
Steps of construction:
- Draw a circle with centre ‘O’ and radius 6 cm.
- Take a point P outside the circle such that OP =10 cm. Join OP.
- Draw the perpendicular bisector to OP which bisects it at M.
- Taking M as centre and PM or MO as radius draw a circle. Let the circle intersects the given circle at A and B.
- Join P to A and B.
- PA and PB are the required tan¬gents of lengths 8 cm each.
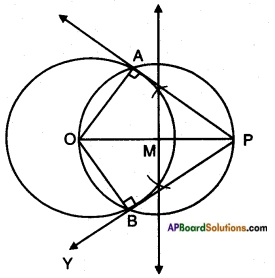 Proof: In △OAP
Proof: In △OAP
OA2 + AP2 = 62 + 82
= 36 + 64 = 100
OP2 = 102 = 100
∴ OA2 + AP2 = OP2
Hence AP is a tangent.
Similarly BP is a tangent.
Question 6.
Construct, a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Answer: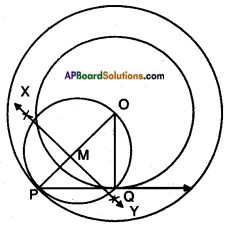 Steps of construction:
Steps of construction:
- Draw two concentric circles with centre ‘O’ and radii 4 cm and 6 cm.
- Take a point ‘P’ on larger circle and join O, P.
- Draw the perpendicular bisector of OP which intersects it at M.
- Taking M as centre and PM or MO as radius draw a circle which intersects smaller circle at Q.
- Join PQ, which is a tangent to the smaller circle.
Question 7.
Draw a circle with the help of a bangle, take a point outside the circle. Con-struct the pair of tangents from this point to the circle measure them. Write conclusion.
Answer: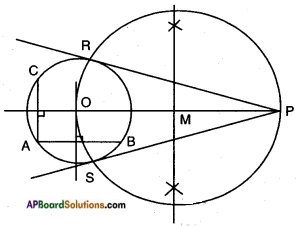 Steps of construction:
Steps of construction:
- Draw a circle with the help of a bangle.
- Draw two chords AB and AC. Perpendicular bisectors of AB and AC meets at ‘O’ which is the centre of the circle.
- Taking an outside point P, join OP.
- Let M be the midpoint of OP. Taking M as centre OM as radius, draw a circle which intersects the given circle at R and S. Join PR, PS which are the required tangents.
Conclusion: Tangents drawn from an external point to a circle are equal.
Question 8.
In a right triangle ABC, a circle with a side AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.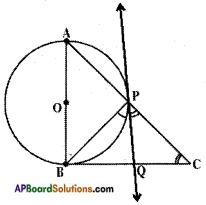 Answer:
Answer:
Let ABC be a right triangle right angled at P.
Consider a circle with diametere AB.
From the figure, the tangent to the circle at B meets BC in Q.
Now QB and QP are two tangents to the circle from the same point P.
QB = QP …….. (1)
Also, ∠QPC = ∠QCP
∴ PQ = QC (2)
From (1) and (2);
QB = QC Hence proved.
Question 9.
Draw a tangent to a given circle with center O from a point ‘R’ outside the circle. How many tangents can be drawn to the circle from that point? [Hint: The distance of two points to the point of contact is the same.
Answer:
Only two tangents can be drawn from a given point outside the circle.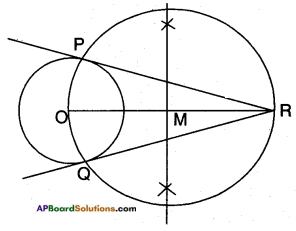
AP Board Textbook Solutions PDF for Class 10th Maths
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF







0 Comments:
Post a Comment