AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Book Answers

AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 8 Similar Triangles Ex 8.1
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 8th Lesson Similar Triangles Ex 8.1 Textbook Questions and Answers

Question 1.
In △PQR, ST is a line such that 𝑃𝑆𝑆𝑄 = 𝑃𝑇𝑇𝑅 and also ∠PST = ∠PRQ.
Prove that △PQR is an isosceles triangle.
Answer:
Given : In △PQR,
𝑃𝑆𝑆𝑄 = 𝑃𝑇𝑇𝑅 and ∠PST= ∠PRQ.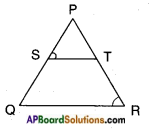

R.T.P: △PQR is isosceles.
Proof: 𝑃𝑆𝑆𝑄 = 𝑃𝑇𝑇𝑅
Hence, ST || QR (Converse of Basic proportionality theorem)
∠PST = ∠PQR …….. (1)
(Corresponding angles for the lines ST || QR)
Also, ∠PST = ∠PRQ ……… (2) given
From (1) and (2),
∠PQR = ∠PRQ
i.e., PR = PQ
[∵ In a triangle sides opposite to equal angles are equal]
Hence, APQR is an isosceles triangle.

Question 2.
In the given figure, LM || CM and LN || CD. Prove that 𝐴𝑀𝐴𝐵 = 𝐴𝑁𝐴𝐷.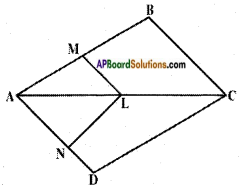

Answer:
Given : LM || CB and LN || CD In △ABC, LM || BC (given) Hence,

Adding ‘1’ on both sides.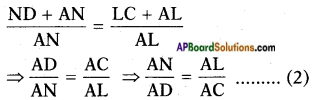

From (1) and (2)
∴ 𝐴𝑀𝐴𝐵 = 𝐴𝑁𝐴𝐷.

Question 3.
In the given figure, DE || AC and DF || AE. Prove that 𝐵𝐹𝐹𝐸 = 𝐵𝐸𝐴𝐶.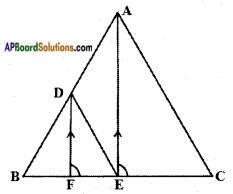

Answer:
In △ABC, DE || AC
Hence 𝐵𝐸𝐸𝐶 = 𝐵𝐷𝐷𝐴 ………. (1)
[∵ A line drawn parallel to one side of a triangle divides the other two sides in the same ratio – Basic proportionality theorem]
Also in △ABE, DF || AE
Hence 𝐵𝐹𝐹𝐸 = 𝐵𝐷𝐷𝐴 ………. (2)
From (1) and (2), 𝐵𝐹𝐹𝐸 = 𝐵𝐸𝐴𝐶 Hence proved.

Question 4.
Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side (Using Basic proportionality theorem).
Answer: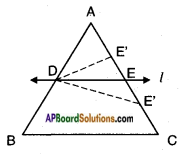

Given: In △ABC; D is the mid-point of AB.
A line ‘l’ through D, parallel to BC, meeting AC at E.
R.T.P: E is the midpoint of AC.
Proof:
DE || BC (Given)
then
𝐴𝐷𝐷𝐵 = 𝐴𝐸𝐸𝐶(From Basic Proportional theorem)
Also given ‘D’ is mid point of AB.
Then AD = DB.
⇒ 𝐴𝐷𝐷𝐵 = 𝐷𝐵𝐷𝐵 = 𝐴𝐸𝐸𝐶 = 1
⇒ AE = EC
∴ ‘E’ is mid point of AC
∴ The line bisects the third side AC⎯⎯⎯⎯⎯⎯⎯⎯.
Hence proved.

Question 5.
Prove that a line joining the mid points of any two sides of a triangle is parallel to the third side. (Using converse of Basic proportionality theorem)
Answer:
Given: △ABC, D is the midpoint of AB and E is the midpoint of AC.
R.T.P : DE || BC.
Proof: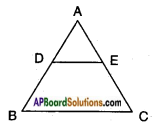

Since D is the midpoint of AB, we have AD = DB ⇒ 𝐴𝐷𝐷𝐵 = 1 ……. (1)
also ‘E’ is the midpoint of AC, we have AE = EC ⇒ 𝐴𝐸𝐸𝐶 = 1 ……. (2)
From (1) and (2)
𝐴𝐷𝐷𝐵 = 𝐴𝐸𝐸𝐶
If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
∴ DE || BC by Basic proportionality theorem.
Hence proved.

Question 6.
In the given figure, DE || OQ and DF || OR. Show that EF || QR.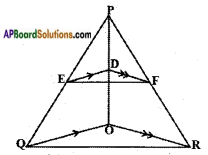

Answer:
Given: △PQR, DE || OQ; DF || OR
R.T.P: EF || QR
Proof:
In △POQ;
𝑃𝐸𝐸𝑄 = 𝑃𝐷𝐷𝑂 ……. (1)
[∵ ED || QO, Basic proportionality theorem]
In △POR; 𝑃𝐹𝐹𝑅 = 𝑃𝐷𝐷𝑂 ……. (2) [∵ DF || OR, Basic Proportionality Theorem]
From (1) and (2),
𝑃𝐸𝐸𝑄 = 𝑃𝐹𝐹𝑅
Thus the line EF⎯⎯⎯⎯⎯⎯⎯ divides the two sides PQ and PR of △PQR in the same ratio.
Hence, EF || QR. [∵ Converse of Basic proportionality theorem]

Question 7.
In the given figure A, B and C are points on OP, OQ and OR respec¬tively such that AB || PQ and AC || PR. Show that BC || QR.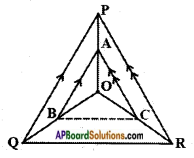

Answer:
Given:
In △PQR, AB || PQ; AC || PR
R.T.P : BC || QR
Proof: In △POQ; AB || PQ
𝑂𝐴𝐴𝑃 = 𝑂𝐵𝐵𝑄 ……… (1)
(∵ Basic Proportional theorem)
and in △OPR, Proof: In △POQ; AB || PQ
𝑂𝐴𝐴𝑃 = 𝑂𝐶𝐶𝑅 ……… (2)
From (1) and (2), we can write
𝑂𝐵𝐵𝑄 = 𝑂𝐶𝐶𝑅
Then consider above condition in △OQR then from (3) it is clear.
∴ BC || QR [∵ from converse of Basic Proportionality Theorem]
Hence proved.

Question 8.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at point ‘O’. Show that𝐴𝑂𝐵𝑂 = 𝐶𝑂𝐷𝑂.
Answer:
Given: In trapezium □ ABCD, AB || CD. Diagonals AC, BD intersect at O.
R.T.P: 𝐴𝑂𝐵𝑂 = 𝐶𝑂𝐷𝑂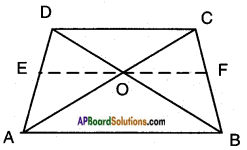

Construction:
Draw a line EF passing through the point ‘O’ and parallel to CD and AB.
Proof: In △ACD, EO || CD
∴ 𝐴𝑂𝐶𝑂 = 𝐴𝐸𝐷𝐸 …….. (1)
[∵ line drawn parallel to one side of a triangle divides other two sides in the same ratio by Basic proportionality theorem]
In △ABD, EO || AB
Hence, 𝐷𝐸𝐴𝐸 = 𝐷𝑂𝐵𝑂
[∵ Basic proportionality theorem]
𝐵𝑂𝐷𝑂 = 𝐴𝐸𝐸𝐷 …….. (2) [∵ Invertendo]
From (1) and (2),
𝐴𝑂𝐶𝑂 = 𝐵𝑂𝐷𝑂
⇒ 𝐴𝑂𝐵𝑂 = 𝐶𝑂𝐷𝑂 [∵ Alternendo]

Question 9.
Draw a line segment of length 7.2 cm and divide it in the ratio 5 : 3. Measure the two parts.
Answer: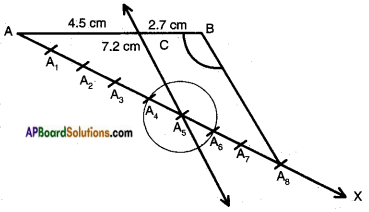

Steps of construction:

Draw a line segment AB⎯⎯⎯⎯⎯⎯⎯⎯ of length 7.2 cm.
Construct an acute angle ∠BAX at A.
Mark off 5 + 3 = 8 equal parts (A₁, A₂, …., A₈) on AX↔ with same radius.
Join A₈ and B.
Draw a line parallel to A8 B↔ at A₅ meeting AB at C.
Now the point C divides AB in the ratio 5:3.
Measure AC and BC. AC = 4.5 cm and BC = 2.7 cm.

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 exam preparation. The AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1, AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook solutions, AP Board Class 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1, AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbook solutions, AP Board STD 10th Maths Chapter 8 Similar Triangles Ex 8.1 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022