 |
| AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Book Answers |
Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbooks Solutions PDF
Andhra Pradesh State Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 10th |
| Subject | Maths |
| Chapters | Maths Chapter 5 Quadratic Equations Ex 5.3 |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Answers.
- Look for your Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions for PDF Free.
AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:10th Class Maths 5th Lesson Quadratic Equations Ex 5.3 Textbook Questions and Answers
Question 1.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
i) 2x2 + x – 4 = 0
Answer:
Given: 2x2 + x – 4 = 0
⇒ 2x2 + x = 4
⇒ (√2x)2 + x = 4
⇒ (√2x)2 + 2.√2.x.122√ = 4
Now LHS is in the form a2 + 2ab
where b = 122√
Adding b2 = (122√)2 on both sides we get

ii) 4x2 + 4√3x + 3 = 0
Answer:
Given: 4x2 + 4√3x + 3 = 0
⇒ 4x2 + 4√3x = -3
⇒ (2x)2 + 2(2x)√3 = -3
LHS is of the form a2 + 2ab where
where b = √3.
∴ Adding b2 = (√3)2 = 3 on both sides, we get
(2x)2 + 2(2x)(√3) + (√3)2 = -3 + (√3)2
⇒ (2x + √3)2 = -3 + 3 = 0
∴ (2x + √3)2 = 0
⇒ 2x + √3 = 0
⇒ 2x = -√3
⇒ x = −3√2
∴ The roots are −3√2, −3√2.
iii) 5x2 – 7x – 6 = 0
Given quardratic equation = 5x2 – 7x – 6 = 0
∴ 5x2 – 7x – 6
⇒ x2 – 75x = 65, it can be re-written as
x2 – 2.710x = 65 now it is in the form
of a2 – 2ab where a = x, and b = 710
Now adding b2 = (710)2 on both sides, we get
Note: If we take the Q.E. as 5x2 – 7x + 6 = 0, then we get the T.B. answer.
iv) x2 + 5 = -6x
Answer:
The given Q.E. is x2 + 5 = -6x
⇒ x2 + 6x = -5
⇒ (x)2 + 2.(x).3 = -5
Now L.H.S. is of the form a2 + 2ab where b = 3.
Adding b2 = 32 on both sides we get
x2 + 2(x)(3) + 32 = -5 + 32
(x + 3)2 = -5 + 9 = 4
∴ x + 3 = 74 = ± 2
⇒ x = +2 – 3 or – 2 – 3
= -1 or -5 are the roots of the given Q.E.
Question 2.
Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula,
i) 2x2 + x – 4 = 0
Answer:
Comparing this Q.E. with ax2 + bx + c = 0
a = 2; b = 1; c = -4
x = −𝑏±𝑏2−4𝑎𝑐√2𝑎
ii) 4x2 + 4√3x + 3 = 0
Answer:
Given: 4x2 + 4√3x + 3 = 0
Here a = 4; b = 4√3 ; c = 3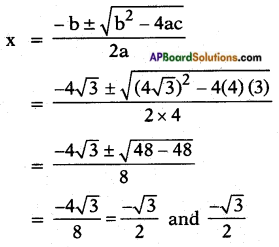
iii) 5x2 – 7x – 6 = 0
Answer:
Given: 5x2 – 7x – 6 = 0
Here a = 5; b = -7 and c = -6
iv) x2 + 5 = -6x
Answer:
Given: x2 + 5 = -6x
⇒ x2 + 6x + 5 = 0
Here a = 1; b = 6; c = 5
Question 3.
Find the roots of the following equations:
i) x – 1𝑥 = 3, x ≠ 0
Answer:
Given: x – 1𝑥 = 3
⇒ x2 + 6x + 5 = 0
⇒ 𝑥2−1𝑥 = 3
⇒ x2 – 1 = 3x
⇒ x2 – 3x – 1 = 0
Here a = 1; b = -3; c = -1
ii) 1𝑥+4 – 1𝑥−7 = 1130, x ≠ -4, 7
Answer:
Given: 1𝑥+4 – 1𝑥−7 = 1130
⇒ x2 – 3x – 28 = -30
⇒ x2 – 3x – 28 + 30 = 0
⇒ x2 – 3x + 2 = 0
⇒ x2 – 2x – x + 2 = 0
⇒ x(x – 2) – 1(x – 2) = 0
⇒ (x – 2) (x – 1) = 0
⇒ x – 2 = 0 (or) x – 1 = 0
⇒ x = 2 or x = 1
⇒ x = 2 or 1.
Question 4.
The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is 13. Find his present age.
Answer:
Let the present age of Rehman be x years.
3 years ago Rehman’s age = x – 3 and its reciprocal is 1𝑥−3
Rehman’s age 5 years from now = x + 5 and its reciprocal is 1𝑥+5
The sum of the reciprocals
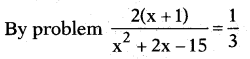
⇒ x2 + 2x – 15 = 3(2x + 2)
⇒ x2 + 2x – 15 = 6x + 6
⇒ x2 + 2x – 15 – 6x – 6 = 0
⇒ x2 – 4x – 21 =0
⇒ x2 – 7x + 3x – 21 =0
⇒ x(x – 7) + 3(x – 7) 0
⇒ (x – 7) (x + 3) = 0
⇒ x – 7 = 0 or x + 3 = 0
⇒ x = 7 or x = -3
But x can’t be negative, x = 7
i.e., Present age of Rehman = 7 years.
Question 5.
In a class test, the sum of Moulika’s marks in Mathematics and English is 30. If she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in the two subjects.
Answer:
Sum of the marks in Mathematics and English = 30
Let Moulika’s marks in Mathematics be x Then her marks in English = 30 – x
If she got 2 more marks in Mathematics, then her marks would be x + 2.
If she got 3 marks less in English then her marks would be 30 – x – 3 = 27 – x
By problem (x + 2) (27 – x) = 210
⇒ x(27 – x) + 2(27 – x) = 210
⇒ 27x – x2 + 54 – 2x = 210
⇒ -x2 + 25x + 54 = 210
⇒ x2 – 25x – 54 + 210 = 0
⇒ x2 – 25x + 156 = 0
⇒ x2 – 12x – 13x + 156 = 0
⇒ x(x – 12) – 13(x 12) = 0
⇒ (x – 12) (x – 13) = 0
⇒ x – 12 = 0 or x – 13 = 0
⇒ x = 12 or x = 13
If x = 12, then marks in Mathematics = 12 English = 30 – 12 = 18
If x = 13, then marks in Mathematics = 13 English = 30 – 13 = 17
Question 6.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Answer:
Let the shorter side of the rectangular field = x m.
Then its longer side = x + 30 m.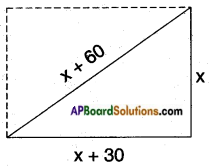
The diagonal of a rectangle is also the hypotenuse of the lower triangle Here the diagonal = x + 60
∴ By Pythagoras Theorem
(side)2 + (side)2 = (hypotenuse)2
⇒ (x + 30)2 + x2 = (x + 60)2
⇒ x2 + 60x + 900 + x2 = x2 + 120x + 3600
⇒ x2 – 60x – 2700 = 0
⇒ x2 – 90x + 30x – 2700 = 0
⇒ x(x – 90) + 30 (x – 90) = 0
⇒ (x – 90) (x + 30) = 0
⇒ x – 90 = 0 (or) x + 30 = 0
⇒ x = +90 (or) x = -30 But ‘x’ can’t be negative.
∴ x = 90 m
i.e., the shorter side x = 90 m Longer side x + 30 = 90 + 30 = 120 m.
Question 7.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Answer:
Let the large number be x.
8 times larger number = Square of the srnall number = 8x
Square of the larger number = x2
By problem, x2 – 8x = 180
⇒ x2 – 8x – 180 = 0
⇒ x2– 18x + 10x – 180 = 0
⇒ x(x – 18) + 10(x – 18) = 0
⇒ (x + 10)(x – 18) = 0
⇒ x + 10 = 0 (or) x – 18 = 0
⇒ x = -10 (or) x = 18
If x = 18, then larger number =18;
(small number)2 = 8 × (+18) = 144
∴ Small number = √144 = 12
The numbers are 18, 12
Note: Discard x = -10.
Question 8.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Answer:
The distance travelled = 360 km.
Let the speed of the train = x kmph.
Time taken to complete a journey = distance speed 
⇒ x2 + 5x = 1800
⇒ x2 + 5x – 1800 = 0
⇒ x2 + 45x – 40x – 1800 = 0
⇒ x(x + 45) – 40(x + 45) = 0
⇒ (x + 45) (x – 40) = 0
x + 45 = 0 or x -40 = 0
x = -45 or x = +40
But x can’t be negative.
∴ The speed of the train = 40 kmph.
Question 9.
Two water taps together can fill a tank in 938 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Answer:
Let the time taken to fill the tank by smaller tap = x (hours)
So the part filled by smaller tap in
1 hour = 1𝑥 × 758 = 758𝑥 ……. (1)
Again then the time taken to fill the tank by larger tap = (x – 10) hours
∴ the part of tank that can be filled by larger tap alone in one hour of time = 1𝑥−10
∴ In 758 hours the part filled by larger tap = 758(1𝑥−10)
∴ By both taps together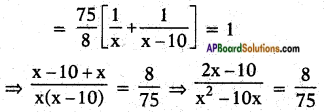
⇒ 150x – 750 = 8x2 – 80x
⇒ 8x2 – 80x – 150x + 750 = 0
⇒ 8x2 – 230x + 750 = 0
⇒ 4x2 – 115x + 375 = 0
⇒ 4x2 – 100x – 15x + 375 = 0
⇒ 4x(x – 25) – 15(x – 25) = 0
∴ (4x – 15) (x – 25) = 0 15
⇒ 4x = 15, x = 154 or x = 25
x = 25 hours.
then time taken to fill by larger tap = x – 10 = 25 – 10 = 15 hours
(x cannot be 154 since we have considered ‘x’ as time taken by smaller tap, which is to be higher one)
Question 10.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speed of the two trains.
Answer:
Let the speed of the passenger train = x kmph.
Then speed of the express train = x + 11 kmph.
Distance travelled = 132 km
We know that time = distance speed 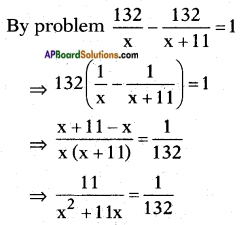
⇒ x2 + 11x = 13 × 11
⇒ x2 + 11x – 1452 = 0
⇒ x2 + 44x – 33x – 1452 = 0
⇒ x(x + 44) – 33 (x + 44) = 0
⇒ (x + 44) (x – 33) = 0
⇒ x + 44 = 0 (or) x – 33 = 0
⇒ x = -44 (or) x = 33
But x can’t be negative.
∴ Speed of the passenger train = x = 33 kmph.
Speed of the express train = x + 11 = 44 kmph.
Question 11.
Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24m, find the sides of the two squares.
(OR)
If the sum of the areas of two squares is 468 m2 and the difference of their perimeters is 24m, then find the measurements of their sides.
Answer:
Let the side of first square = x m say Then perimeter of the first square = 4x [∵ P = 4 . side]
By problem, perimeter of the second square = 4x + 24 (or) 4x – 24
∴ Side of the second square =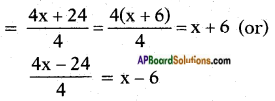
Now sum of the areas of the two squares is given as 468 m2
x2 + (x + 6)2 = 468
⇒ x2 + x2 + 12x + 36 = 468
⇒ 2x2 + 12x + 36 – 468 = 0
⇒ 2x2 + 12x – 432 = 0
⇒ x2 + 6x – 216 = 0
⇒ x2 + 18x – 12x – 216 = 0
⇒ x(x + 18)- 12(x + 18) = 0
⇒ (x + 18) (x – 12) = 0
⇒ x + 18 = 0 (or) x – 12 = 0
⇒ x = -18 (or) 12
But x can’t be negative.
∴ x = 12
i.e., side of the first square = 12
∴ Perimeter = 4 × 12 = 48
∴ Perimeter of the second square = 48 + 24 = 72
∴ Side of the second square = 724 = 18 m.
(or)
x2 + (x – 6)2 = 468
⇒ x2 + x2 – 12x + 36 = 468
⇒ 2x2 – 12x – 432 – 0
⇒ x2 – 6x – 216 = 0
⇒ x2 – 18x + 12x – 216 = 0
⇒ x(x-18) + 12(x-18) = 0
⇒ (x – 18) (x + 12) = 0
⇒ x – 18 = 0 (or) x + 12 = 0
⇒ x = 18 (or) – 12
But x can’t be negative.
∴ x = 18
i.e., side of the first square = 18 m
∴ Perimeter = 4 × 18 = 72
Perimeter of the second square = 72 – 24 = 48
∴ Side of the second square = 484 = 12 m.
i.e., In any way, the sides of the squares are 12m, 18m.
Question 12.
If a polygon of ‘n’ sides has 12n(n – 3) diagonals. How many sides will a polygon having 65 diagonals? Is there a polygon with 50 diagonals?
Answer:
Given: Number of diagonals of a polygon with n-sides = 𝑛(𝑛−3)2
No. of diagonals of a given polygon = 65
i.e., 𝑛(𝑛−3)2 = 65
where n is number of sides of the polygon
⇒ n2 – 3n = 2 × 65
⇒ n2 – 3n – 130 = 0
⇒ n2 – 13n + 10n – 130 = 0
⇒ n(n – 13) + 10(n – 13) = 0
⇒ (n – 13) (n + 10) = O
⇒ n – 13 = 0 (or) n + 10 = 0
⇒ n = 13 (or) n = -10
But n can’t be negative.
∴ n = 13 (i.e.) number of sides = 13.
Also to check 50 as the number of diagonals of a polygon
∴ 𝑛(𝑛−3)2 = 50
⇒ n2 – 3n = 100
⇒ n2 – 3n – 100 = 0
There is no real value of n for which the above equation is satisfied.
∴ There can’t be a polygon with 50 diagonals.
AP Board Textbook Solutions PDF for Class 10th Maths
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF







0 Comments:
Post a Comment