AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Book Answers

AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Book Answers

AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles InText Questions books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 8 Similar Triangles InText Questions book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 8 Similar Triangles InText Questions
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions Answers PDF Online?

1. Visit our website - Hsslive
2. Click on the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Answers.
3. Look for your Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks PDF.
4. Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 8th Lesson Similar Triangles InText Questions and Answers

Do these

(Page No. 194)

Question 1.
Fill in the blanks with similar/not similar.
i) All squares are ………. (similar)
ii) All equilateral triangles are ………. (similar)
iii) All isosceles triangles are ………. (similar)
iv) Two polygons with same number of sides are ………, if their corresponding angles are equal and corresponding sides are equal. (similar)
v) Reduced and enlarged photographs of an object are ………. (similar)
vi) Rhombus and squares are ……… to each other. (not similar)

Question 2.
Write True / False for the following statements.
i) Any two similar figures are congruent.
Answer:
False
ii) Any two congruent figures are similar.
Answer:
True
iii) Two polygons are similar if their corresponding angles are equal.
Answer:
False

Question 3.
Give two different examples of pair of
i) Similar figures
ii) Non-similar figures
Answer:
i) Similar figures:
a) Any two circles
b) Any two squares
c) Any two equilateral triangles
ii) Non-similar figures:
a) A square and a rhombus
b) A square and a rectangle

Question 4.
What value(s) of x will make DE || AB, in the given figure? (Page No. 200)
AD = 8x + 9, CD = x + 3,
BE = 3x + 4, CE = x.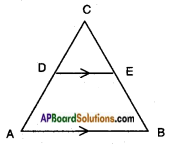

Answer:
Given : In AABC, DE // AB AD = 8x + 9, CD = x + 3,
BE = 3x + 4, CE = x
By Basic proportionality theorem,
If DE // AB then we should have
CDDA = CEEB
𝑥+38𝑥+9 = 𝑥3𝑥+4
⇒ (x + 3) (3x + 4) = x (8x + 9)
⇒ x (3x + 4) + 3 (3x + 4) – 8x² + 9x
⇒ 3x² + 4x + 9x + 12 = 8x² + 9x
⇒ 8x² + 9x – 3x² – 4x – 9x -12 = 0
⇒ 5x² – 4x – 12 = 0
⇒ 5x² – 10x + 6x – 12 = 0
⇒ 5x (x – 2) + 6 (x – 2) = 0
⇒ (5x + 6) (x – 2) = 0
⇒ 5x + 6 = 0 or x – 2 = 0
⇒ x = −65 or x = 2;
x cannot be negative.
∴ The value x = 2 will make DE // AB.

Question 5.
In △ABC, DE || BC. AD = x, DB = x – 2, AE = x + 2 and EC = x – 1. Find the value of x. (Page No. 200)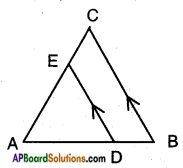

Answer:
Given: In △ABC, DE // BC
∴ By Basic proportionality theorem, we have
ADDB = AEEC
xx−2 = 𝑥+2𝑥−1
⇒ x (x – 1) = (x + 2) (x – 2)
⇒ x² – x = x² – 4
⇒ -x = -4
∴ x = 4

Try This

Question 1.
E and F are points on the sides PQ and PR respectively of △PQR. For each of the following, state whether EF || QR or not? (Page No. 197)
i) PE = 3.9 cm, EQ = 3 cm,
PF = 3.6 cm and FR = 2.4 cm.
Answer: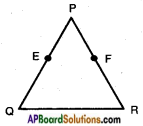

Here
PEEQ = 3.93 = 1.31
PFFR = 3.62.4 = 32
PEEQ ≠ PFFR
Hence, EF is not parallel to QR.

ii) PE = 4 cm, QE = 4.5 cm,
Answer:
Here
PEEQ = 44.5 = 89
PFRF = 89
PEEQ = PFRF
∴ EF // QR
Hence, EF is parallel to QR.

iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 1.8 cm and PF = 3.6 cm.
Answer: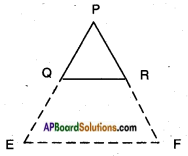

Given: PQ = 1.28 cm, PE = 1.8 cm
⇒ EQ = PE – PQ = 1.8 – 1.28
⇒ EQ = 0.52 cm
Also, PR = 2.56 cm, PE = 3.6 cm, FR = PF – PR = 3.6 cm – 2.56 cm
FR = 1.04 cm

∴ EF // QR (By converse of Basic proportionality theorem)
Hence, EF is parallel to QR.

Question 2.
In the following figures DE || BC. (Page No. 198)
i) Find EC.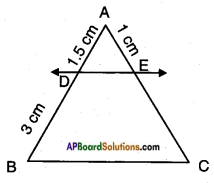

Answer:
ADDB = 𝐴𝐸𝐸𝐶
⇒ 1.53 = 1𝐸𝐶
∴ EC = 31.5 = 2 cm

ii) Find AD.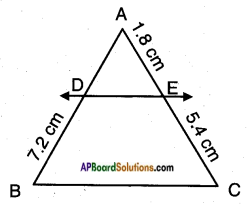

Answer:

Think & Discuss

Question 1.
Can you give some more examples from your daily life where scale factor is used? (Page No. 192)
Answer:
Scale factor is used in drawing maps, designing machines and in sculpture, etc.

Question 2.
Can you say that a square and a rhombus are similar? Discuss with your friends.Write why the conditions are not sufficient. (Page No. 193)
Answer:
A square □ ABCD and a rhombus ▱ PQRS are not similar.
Though the ratio of their corresponding sides are equal, the corresponding angles are not equal.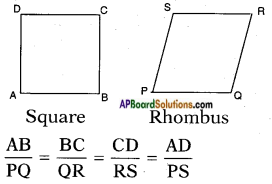

but ∠A ≠ ∠P; ∠B ≠ ∠Q
∠C ≠ ∠R; ∠D ≠ ∠S

Try This

(Page No. 207)

Question 1.
Are the triangles similar ? If so, name the criterion of similarity. Write the similarity relation in symbolic form.
i)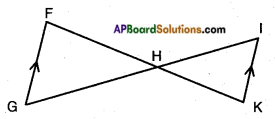

!! ∠G = ∠I alt. int. angles for the ∠F = ∠K parallel lines GF // KI
Answer:
∠FHG = ∠IHK (Vertically opp. angle)
∴ ∠GHF and ∠IKH are similar by AAA similarity rule.
△GHF ~ △IKH.

ii)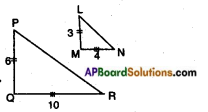

Answer:
𝑃𝑄𝐿𝑀 = 63 = 2;
𝑄𝑅𝑀𝑁 = 104 = 2.5;
𝑃𝑄𝐿𝑀 ≠ 𝑄𝑅𝑀𝑁
△PQR and △LMN are not similar.
△PQR ~ △LMN

iii)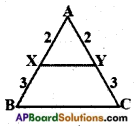

Answer:
∠A = ∠A (Common)
𝐴𝐵𝐴𝑋 = 53; 𝐴𝐶𝐴𝑌 = 53
∴ △ABC and △AXY are similar by SAS similarity condition.
△ABC ~ △AXY.

iv)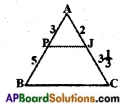

Answer:

∴ △ABC and △APJ are not similar.

v)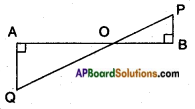

Answer:
∠A = ∠B = 90°
∠AOQ = ∠POB (∵ Vertically opposite angles)
∠Q = ∠P (alternate interior angles)
∴ △AOQ and △BOP are similar by AAA criterion.
△AOQ ~ △BOP.

vi)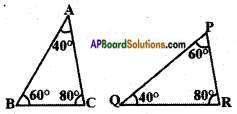

Answer:
△ABC and △QPR are similar by AAA similarity condition.
△ABC ~ △QPR.

vii)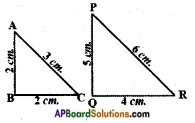

Answer:
∠A = ∠P
𝐴𝐵𝑃𝑄 = 25; 𝐴𝐶𝑃𝑅 = 36 = 12
∴ 𝐴𝐵𝑃𝑄 ≠ 𝐴𝐶𝑃𝑅
Hence not similar.

viii)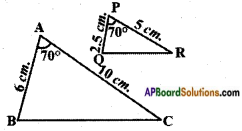

Answer:
𝐴𝐵𝑃𝑄 = 62.5; 𝐴𝐶𝑃𝑅 = 105
∴ △ABC and △PQR are not similar.

Question 2.
Explain why the triangles are similar and then find the value of x.
i)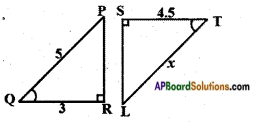

Answer:
Given: In △PQR and △LTS
∠Q = ∠T; ∠R = ∠S = 90°
∴ ∠P = ∠T
(by angle sum property of triangles)
Hence, △PQR ~ △LTS [∵ AAA]

ii)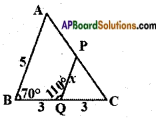

Answer:
Given: In △ABC and △PQC
∠B = ∠Q
[∵ ∠PQC = 180°- 110° = 70° – linear pair of angles]
∠C = ∠C [∵ Common]
∠A = ∠P [∵ Angle Sum property of triangles]
△ABC ~ △PQC by AAA similarity condition.
Then the ratio of their corresponding sides are equal.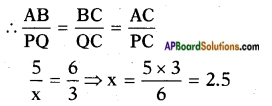

iii)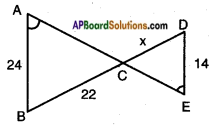

Answer:
Given: In △ABC and △ECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite]
∴ ∠B = ∠D [∵ angle sum property]
∴ △ABC ~ △EDC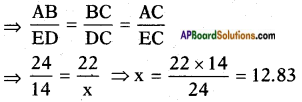

iv)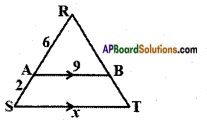

Answer:
Given: In △RAB and △RST
∠R = ∠R (common)
∠A = ∠S and ∠B = ∠T
[∵ Pair of corresponding angles for AB // ST]
∴ △RAB ~ △RST [∵ AAA similarity]

v)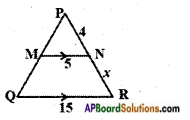

Answer:
Given: In △PQR and △PMN
∠P = ∠P [∵ Common]
∠Q = ∠M [∵ Pair of corresponding angles for MN // QR]
∠R = ∠N
△PQR ~ △PMN [∵ AAA similarity]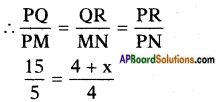

[From the figure, PR = 4 + x]
⇒ 3 × 4 = 4 + x
⇒ x = 12 – 4 = 8

vi)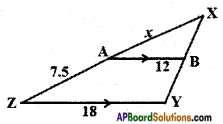

Answer:
Given: In △XYZ and △XBA,
∠X = ∠X [∵ Common]
∠B = ∠Y [∵ Pair of corresponding ∠A = ∠Z angles for AB // ZY]
∴ △XYZ ~ △XBA [∵ AAA similarity]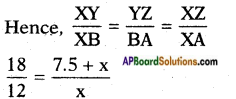

[From the figure, XZ = 7.5 + x]
32 = 7.5+xx
3x = 15 + 2x;
3x – 2x = 15
x = 15

vii)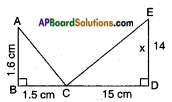

Answer:
Given: With the given conditions, we can’t find the value of x.
Note: If it is given that ∠A = ∠E then
we can say that △ABC ~ △EDC by AAA rule

viii)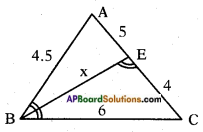

Answer:
In △ABC and △BEC
∠ABC = ∠CEB (given)
∠C = ∠C (Common angle)
∴ △ABC ~ △BEC
(A.A. Criterion similarity)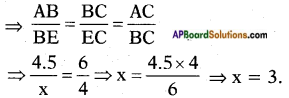

Think & Discuss

(Page No. 203)

Question 1.
Discuss with your friends that in what way similarity of triangles is dif¬ferent from similarity of other polygons?
Answer:
In two triangles if the corresponding angles are equal then they are similar, whereas in two polygons if the corre-sponding angles are equal, they may not be similar, i.e., In triangles,
(Pairs of corresponding angles are equal) ⇔ (Ratio of corresponding sides are equal).
But this is not so with respect to polygons.

Do This

Question 1.
In △ACB, ∠C = 90° and CD ⊥ AB. Prove that BC2AC2 = 𝐵𝐷𝐴𝐷. (Page No. 218)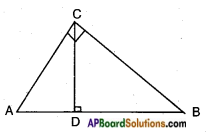

Answer:
Proof: △ADC and △CDB are similar.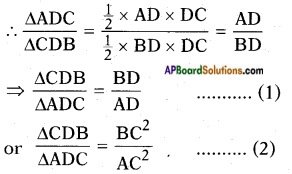

[Ratio of areas of similar triangles is equal to the ratio of squares of their corresponding sides.]
From (1) and (2),
𝐵𝐷𝐴𝐷 = BC2AC2 (Q.E.D.)

Question 2.
A ladder 15 m long reaches a window which is 9 m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12 m high. Find the width of the street. (Page No. 218)
Answer: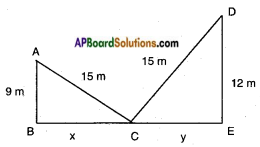

Let A and D be the windows on the either sides of the street.
From Pythagoras theorem,
AC² = AB² + BC²
15² = 9² + BC²
BC² = 225 – 81
BC = √144 = 12 ….. (1)
Also, CD² = DE² + CE²
15² = 12² + CE²
CE² = 225 – 144
CE = √81 = 9
∴ BE = BC + CE = 12 + 9 = 21
Width of the street = 21 m.

Question 3.
In the given figure if AD ⊥ BC, prove that AB² + CD² = BD² + AC². (Page No. 219)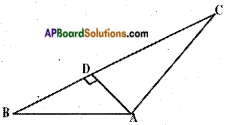

Answer:
Given: In △ABC, AD ⊥ BC.
R.T.P: AB² + CD² = BD² + AC²
Proof: △ABD is a right angled triangle
AB² – BD² = AD² ……. (1)
△ACD is a right angle triangle
AC² – CD² = AD²
From (1) and (2)
AB² – BD² = AC² – CD²
AB² + CD² = BD² + AC²

Think & Discuss

Question 1.
For a right angled triangle with integer sides atleast one of its measurements must be an even number. Why? Discuss this with your friends and teachers. (Page No. 215)
Answer: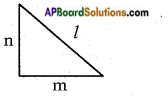

Let l, m, n are integer sides of a right
angled triangle.
then l² – m² + n²
⇒ n = l² – m² = (l + m) (l – m)
Now
Case I: Both l, m are even the (l + m) is even then (l + m) (l – m) is also even. So ‘n’ is even. Here all are even.
Case II: Both l, m are odd then (l + m) and (l – m) become even. Then the product of even numbers is even so ‘n’ is even.
Here only ‘n’ is even.
Case III: If we consider l is even, m is’ odd then ‘n’ will be odd. So here T is even. We observe in all above three cases at least one of l, m, n is even; Hence proved.

AP Board Textbook Solutions PDF for Class 10th Maths

• AP Board Class 10 10th Textbook Solutions PDF
• AP Board Class 10 Maths Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
• AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions exam preparation. The AP Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 8 Similar Triangles InText Questions Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions

How to get AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles InText Questions, AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles InText Questions, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbook solutions, AP Board Class 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles InText Questions, AP Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles InText Questions, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Textbook solutions, AP Board STD 10th Maths Chapter 8 Similar Triangles InText Questions Textbooks Solutions,