AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Book Answers

AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 8 Similar Triangles Optional Exercise
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 8th Lesson Coordinate Geometry Optional Exercise Textbook Questions and Answers

Question 1.
In the given figure, 𝑄𝑇𝑃𝑅 = 𝑄𝑅𝑄𝑆 and ∠1 = ∠2. Prove that △PQS ~ △TQR.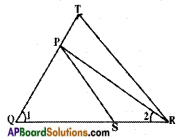

Answer:
Given: 𝑄𝑇𝑃𝑅 = 𝑄𝑅𝑄𝑆
∠1 = ∠2
R.T.P : △PQS ~ △TQR
Proof: In △PQR; ∠1 = ∠2 Thus, PQ = PR
[∵ sides opp. to equal angles are equal]
𝑄𝑇𝑃𝑅 = 𝑄𝑅𝑄𝑆 ⇒ 𝑄𝑇𝑃𝑄 = 𝑄𝑅𝑄𝑆
i.e., the line PS divides the two sides QT and QR of △TQR in the same ratio.
Hence, PS // TR.
[∵ If a line join of any two points on any two sides of triangle divides the two sides in the same ratio, then the line is parallel to the third side]
Hence, PS // TR (converse of B.P.T)
Now in △PQS and △TQR
∠QPS = ∠QTR
[∵ ∠P, ∠T are corresponding angles for PS // TR]
∠QSP = ∠QRT
[∵ ∠S, ∠R are corresponding angles for PS // TR]
∠Q = ∠Q (common)
∴ △PQS ~ △TQR (by AAA similarity)

Question 2.
Ravi is 1.82 m tall. He wants to find the height of a tree in his backyard. From the tree’s base he walked 12.20 m. along the tree’s shadow to a position where the end of his shadow exactly overlaps the end of the tree’s shadow. He is now 6.10 m from the end of the shadow. How tall is the tree?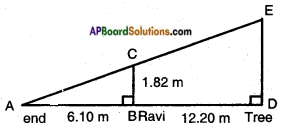

Answer:
Given:
Height of Ravi ‘BC’ = 1.82 m.
Distance of Ravi from the foot of the tree BD = 12.2 m.
Length of the shadow of Ravi = AB = 6.10 m
Let DE represent the tree.
From the figure, △ABC ~ △ADE.
Thus, 𝐴𝐵𝐴𝐷 = 𝐵𝐶𝐷𝐸 = 𝐴𝐶𝐴𝐸
Ratio of corresponding sides of two similar triangles are equal]
6.106.10+12.20 = 1.82DE
DE = 1.82×18.306.10 = 5.46 m
Thus the height of the tree = 5.46 m.

Question 3.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where ‘P’ is any point on side AB. Prove that CQ × PQ = QA × QD.
Answer: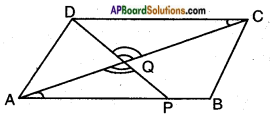

Given: □ ABCD is a parallelogram.
P is a point on AB.
DP and AC intersect at Q.
R.T.P.: CQ . PQ = QA . QD.
Proof: In △CQD, △AQP
∠QCD = ∠QAP
∠CQD = ∠AQP
∴ ∠QDC = ∠QPA
(∵ Angle sum property of triangles)
Thus, △CQD ~ △AQP by AAA similarity condition.
𝐶𝑄𝐴𝑄 = 𝑄𝐷𝑄𝑃 = 𝐶𝐷𝐴𝑃
[∵ Ratio of corresponding sides of similar triangles are equal]
𝐶𝑄𝐴𝑄 = 𝑄𝐷𝑄𝑃
CQ . PQ = QA . QD [Q.E.D]

Question 4.
△ABC and △AMP are two right triangles right angled at B and M respectively. Prove that (i) △ABC ~ △AMP (ii) 𝐶𝐴𝑃𝐴 = 𝐵𝐶𝑀𝑃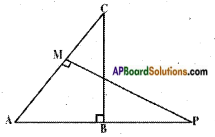

Answer:
Given: △ABC; ∠B = 90°
AAMP; ∠M = 90°
R.T.P : i) △ABC ~ △AMP
Proof: In △ABC and △AMP
∠B = ∠M [each 90° given]
∠A = ∠A [common]
Hence, ∠C = ∠P
[∵ Angle sum property of triangles]
∴ △ABC ~ △AMP (by A.A.A. similarity)
ii) △ABC ~ △AMP (already proved)
𝐴𝐵𝐴𝑀 = 𝐵𝐶𝑀𝑃 = 𝐶𝐴𝑃𝐴
[∵ Ratio of corresponding sides of similar triangles are equal]
𝐶𝐴𝑃𝐴 = 𝐵𝐶𝑀𝑃

Question 5.
An aeroplane leaves an airport and flies due north at a speed of 1000 kmph. At the same time another aeroplane leaves the same airport and flies due west at a speed of 1200 kmph. How far apart will the two planes be after 112 hour?
Answer: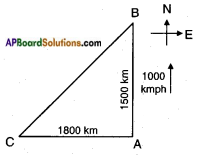

Given: Speed of the first plane due north = 1000 kmph.
Speed of the second plane due west = 1200 kmph.
Distance = Speed × Time
Distance travelled by the first plane in
112 hrs = 1000 × 112 = 1000 × 32 = 1500 km.
Distance travelled by the second plane
in 112 hrs = 1200 × 32 = 1800 km.
From the figure, △ABC is a right triangle; ∠A = 90°.
AB² + AC² = BC²
[Pythagoras theorem]
1500² + 1800² = BC²
2250000 + 3240000 = BC²
∴ BC = √5490000
= 100 × √549 m
≅ 100 × 23.43
≅ 2243km.

Question 6.
In a right triangle ABC right angled at C. P and Q are points on sides AC and CB respectively which divide these sides in the ratio of 2:1. Prove that
i) 9AQ² = 9AC² + 4BC²
ii) 9BP² = 9BC² + 4AC²
iii) 9(AQ² + BP²) = 13AB²
Answer:

Given: In △ABC; ∠C = 90°
R.T.P.: i) 9AQ² = 9AC² + 4BC²
Proof: In △ACQ; ∠C = 90°
AC² + CQ² = AQ²
[side² + side² = hypotenuse²]
AQ² = AC² + (23BC)2
[∵ Q divides CB in the ratio 2 : 1
CQ = 23BC]
AQ² = AC² + 49BC2
AQ² = 9AC2+4BC29
⇒ 9AQ² = 9AC² + 4BC²

ii) 9BP² = 9BC² + 4AC²
Proof: In △PCB,
PB² = PC² + BC² [Pythagoras theorem]

⇒ PB² = AC² + 9BC²
[!! If we take P on CA, in the ratio 2 : 1 then we get
BP² = PC² + BC²
BP² = (23A)2 + BC²
BP² = 49AC2 + BC²
BP² = 4AC2+9BC29
9BP² = 4AC² + 9BC²

iii) 9 (AQ² + BP²) = 13 AB²
Proof: In △ABC,
AC² + BC² = AB²
[Pythagoras theorem]
Also, from (i) and (ii),

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise exam preparation. The AP Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions

How to get AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise, AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise, Andhra Pradesh State Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook solutions, AP Board Class 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise, AP Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise, Andhra Pradesh State Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbook solutions, AP Board STD 10th Maths Chapter 8 Similar Triangles Optional Exercise Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022