AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Book Answers

June 09, 2022 AP State Board No comments

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Book Answers

AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables Ex 4.1 Textbook Questions and Answers

Question 1.
By comparing the ratios 𝑎1𝑎2, 𝑏1𝑏2, 𝑐1𝑐2 K find out whether the lines represented by the following pairs of linear equations intersect at a point, are parallel or are coincident.
a) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
Answer:
Given: 5x – 4y + 8 = 0
7x + 6y – 9 = 0
𝑎1𝑎2 = 57; 𝑏1𝑏2 = −46; 𝑐1𝑐2 = 8−9
∴ 𝑎1𝑎2 ≠ 𝑏1𝑏2
Hence the given pair of linear equations represents a pair of intersecting lines.

b) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Answer:
Given : 9x + 3y + 12 = 0
18x + 6y + 24= 0
𝑎1𝑎2 = 918 = 12;
𝑏1𝑏2 = 36 = 12;
𝑐1𝑐2 = 1224 = 12
∴ 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2
The lines are coincident.

c) 6x – 3y + 10 = 0
2x – y + 9 = 0
Answer:
Given: 6x – 3y + 10 = 0
2x – y + 9 = 0
𝑎1𝑎2 = 62 = 31;
𝑏1𝑏2 = −3−1 = 31;
𝑐1𝑐2 = 109
Here 𝑎1𝑎2 = 𝑏1𝑏2 ≠ 𝑐1𝑐2
∴ The lines are parallel.

Question 2.
Check whether the following equations are consistent or inconsistent. Solve them graphically. (AS2, AS5)
a) 3x + 2y = 8
2x – 3y = 1
Answer:
Given equaions are 3x + 2y = 8 and 2x – 3y = 1
𝑎1𝑎2 = 32;
𝑏2𝑏−3 = −46;
𝑎1𝑎2 ≠ 𝑏1𝑏2
Hence the linear equations are consistent.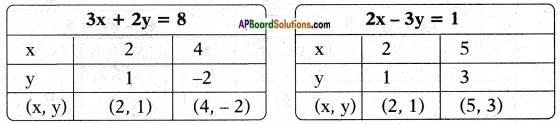

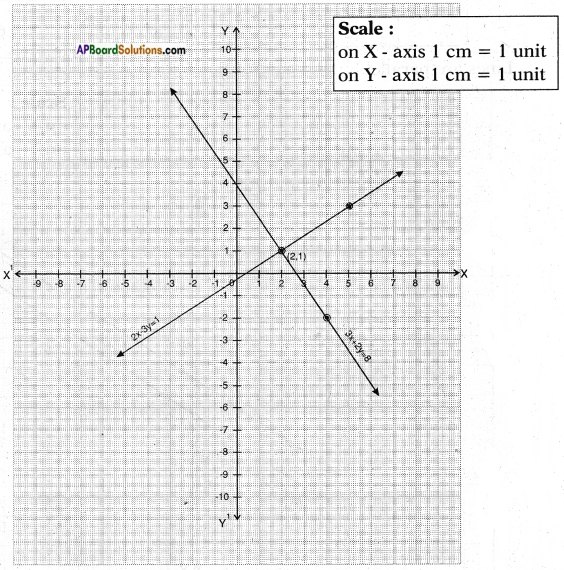
The lines intersect at (2, 1), so the solution is (2, 1).

b) 2x – 3y = 8
4x – 6y = 9
Answer:
Given: 2x – 3y = 8 and 4x – 6y = 9
𝑎1𝑎2 = 24 = 12;
𝑏1𝑏2 = −3−6 = 12;
𝑐1𝑐2 = 89
∴ 𝑎1𝑎2 = 𝑏1𝑏2 ≠ 𝑐1𝑐2
Lines are inconsistent and have no solution.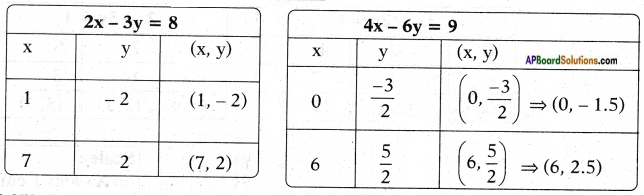

Lines are parallel.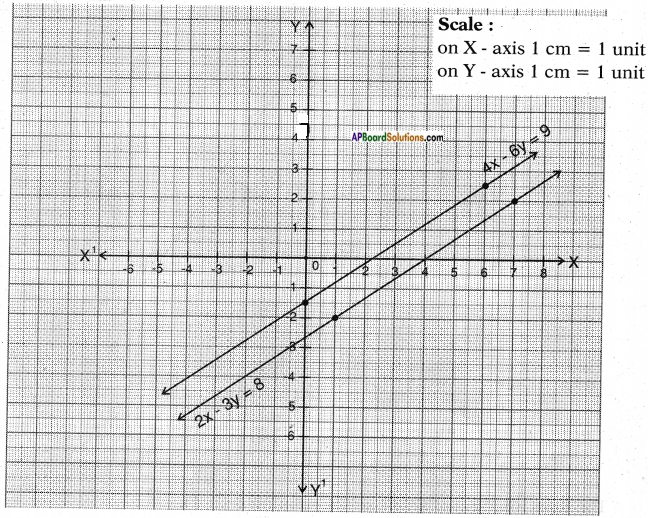

The lines are parallel and no solution exists.

c) 32x + 53y = 7
9x – 10y = 12
Answer:
Given pair of equations 32x + 53y = 7 and 9x – 10y = 12
Now take 32x + 53y = 7 ⇒ 9𝑥+10𝑦6 = 7 ⇒ 9x + 10y = 42
and 9x – 10y =12
𝑎1𝑎2 = 99 = 11;
𝑏1𝑏2 = 10−10 = 1−1 and
𝑐1𝑐2 = −42−12 = 72
Since 𝑎1𝑎2 ≠ 𝑏1𝑏2 they are intersecting lines and hence consistent pair of linear equations.

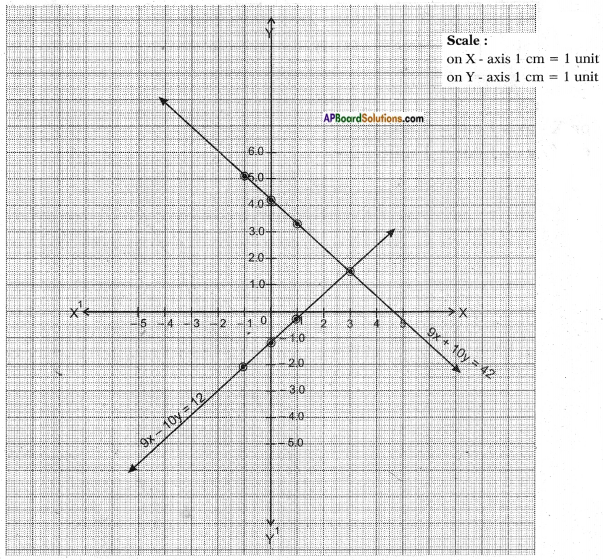
Solution: The unique solution of given pair of equations is (3.1, 1.4)

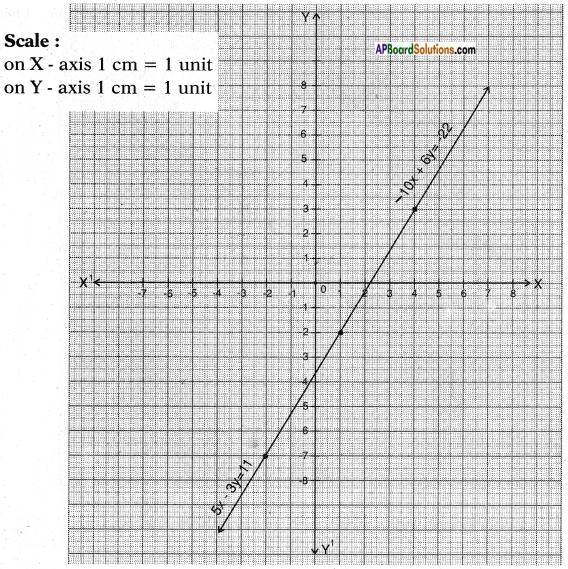
d) 5x – 3y = 11
-10x + 6y = -22
Answer:
Given pair of equations 5x – 3y = 11 and -10x + 6y = -22
𝑎1𝑎2 = 5−10 = −12;
𝑏1𝑏2 = −36 = −12 and
𝑐1𝑐2 = 11−22 = −12
∴ 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2
∴ The lines are consistent.
∴ The given linear equations represent coincident lines.
Thus they have infinitely many solutions.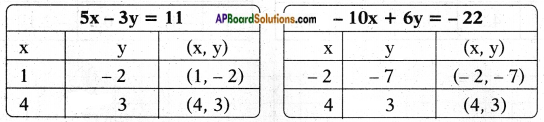

e) 43x + 2y = 8
2x + 3y = 12
Answer:
Given pair of equations 43x + 2y = 8 ⇒ 4𝑥+6𝑦3 = 8 ⇒ 4x + 6y = 24 ⇒ 2x + 3y = 12
𝑎1𝑎2 = 42 = 2;
𝑏1𝑏2 = 63 = 2;
𝑐1𝑐2 = 2412 = 2
∴ 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2
Thus the equations are consistent.
∴ The given equations have infinitely many solutions.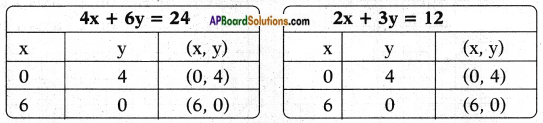

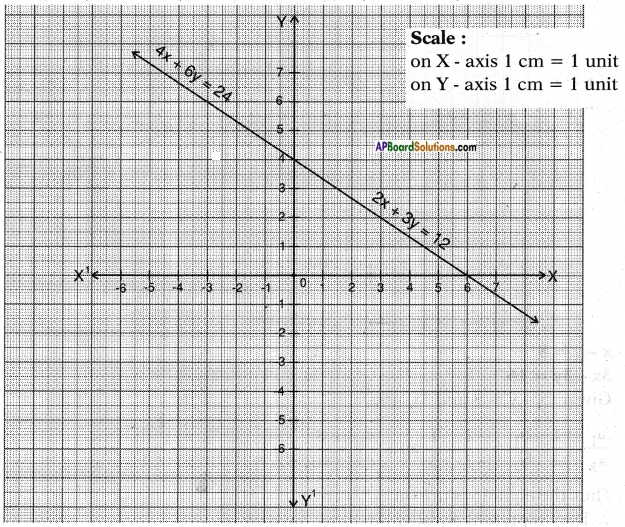
f) x + y = 5
2x + 2y = 10
Answer:
Given pair of equations x + y = 5 and 2x + 2y = 10
𝑎1𝑎2 = 12;
𝑏1𝑏2 = 12;
𝑐1𝑐2 = 510 = 12
∴ 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2
Thus the equations are consistent and have infinitely many solutions.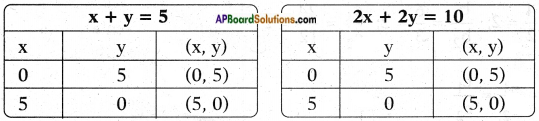

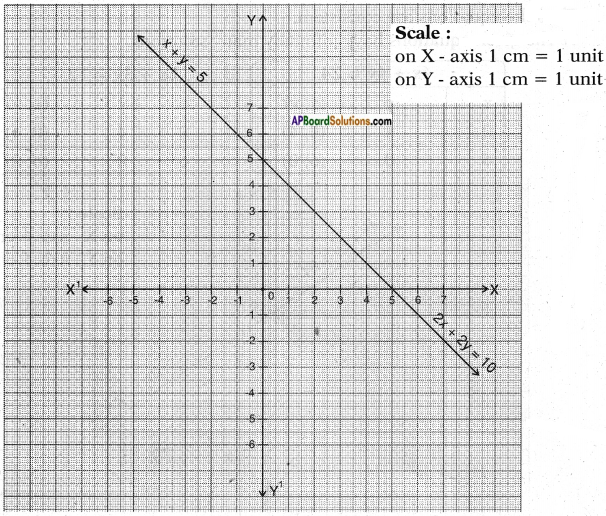
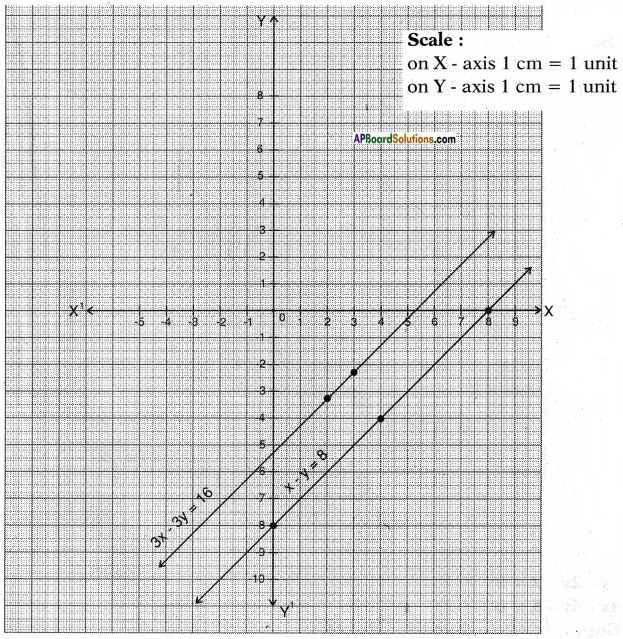
g) x – y = 8
3x – 3y = 16
Answer:
Given pair of equations x – y = 8 and 3x – 3y = 16
𝑎1𝑎2 = 13;
𝑏1𝑏2 = −1−3 = 13 and
𝑐1𝑐2 = 816 = 12
∴ 𝑎1𝑎2 = 𝑏1𝑏2 ≠ 𝑐1𝑐2
Thus the equations are inconsistent.
∴ They represent parallel lines and have no solution.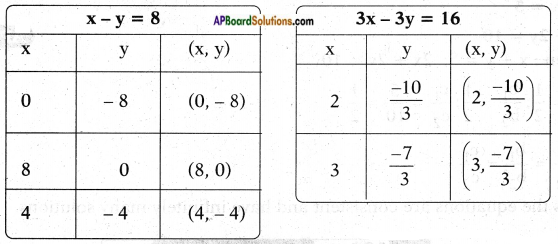

h) 2x + y – 6 = 0 and 4x – 2y – 4 = 0
Answer:
Given pair of equations 2x + y – 6 = 0 and 4x – 2y – 4 = 0
𝑎1𝑎2 = 24 = 12;
𝑏1𝑏2 = 1−2 = −12;
𝑐1𝑐2 = −6−4 = 32
∴ 𝑎1𝑎2 ≠ 𝑏1𝑏2
The equations are consistent.
∴ They intersect at one point giving only one solution.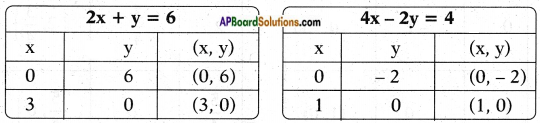

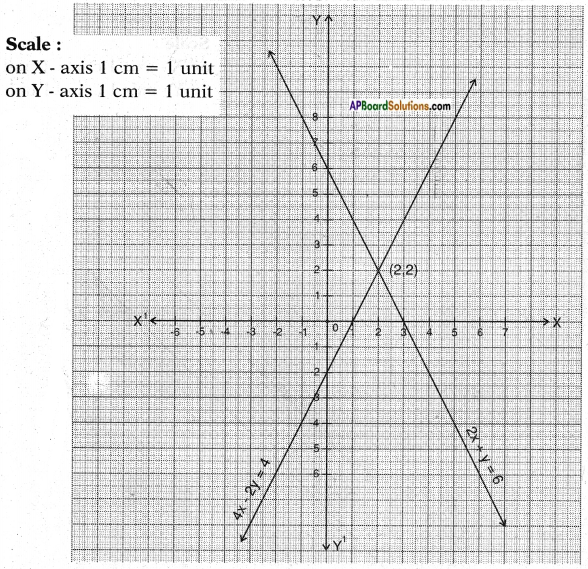
The solution is x = 2 and y = 2

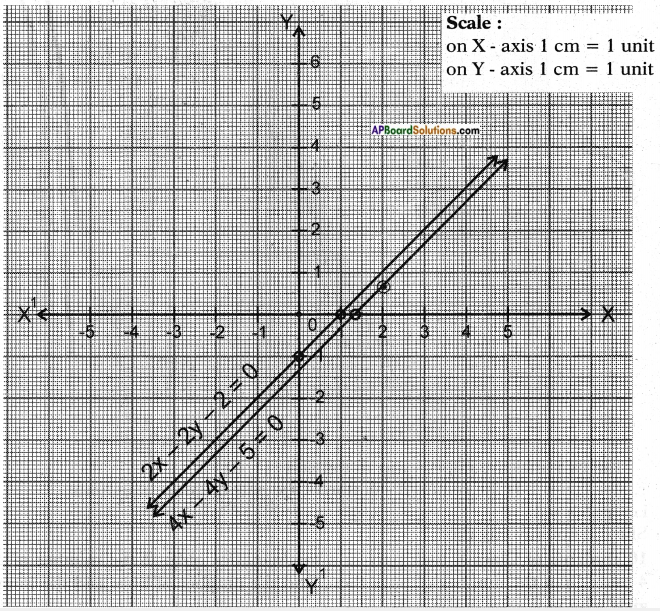
i) 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0
Answer:
Given pair of equations 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0
𝑎1𝑎2 = 24 = 12;
𝑏1𝑏2 = −2−4 = 12;
𝑐1𝑐2 = −2−5 = 25
∴ 𝑎1𝑎2 = 𝑏1𝑏2 ≠ 𝑐1𝑐2
Thus the equations are inconsistent.
∴ They represent parallel lines and have no solution.

Question 3.
Neha went to a ‘sale’ to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered “The number of skirts are two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number of pants purchased.”
Help her friend to find how many pants and skirts Neha bought.
Answer:
Let the number of pants = x and the number of skirts = y
By problem y = 2x – 2 ⇒ 2x – y = 2
y = 4x – 4 ⇒ 4x – y = 4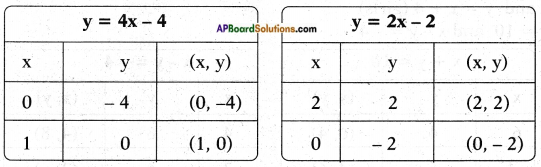

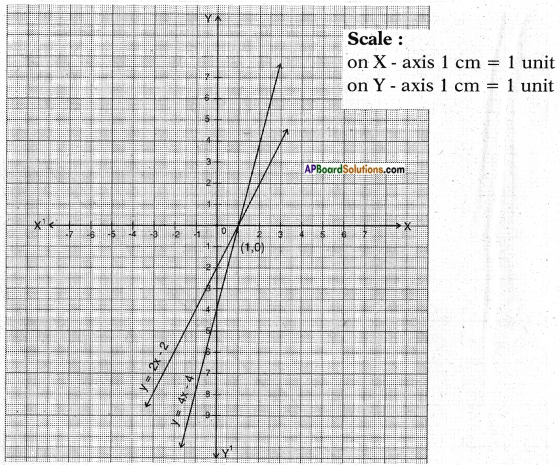
The two lines are intersecting at the point (1,0)
∴ x = 1; y = 0 is the required solution of the pair of linear equations.
i.e., pants =1
She did not buy any skirt.

Question 4.
10 students of Class-X took part in a mathematics quiz. If the number of girls is 4 more than the number of boys then, find the number of boys and the number of girls who took part in the quiz.
Answer:
Let the number of boys be x.
Then the number of girls = x + 4
By problem, x + x + 4 = 10
∴ 2x + 4 = 10
2x = 10-4
x = 62 = 3
∴ Boys = 3 Girls = 3 + 4 = 7 (or)
Boys = x, Girls = y
By problem x + y = 10 (total)
and y = x + 4 (girls)
⇒ x + y = 10 and x – y = – 4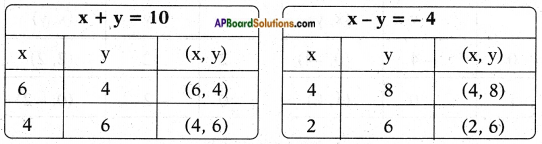

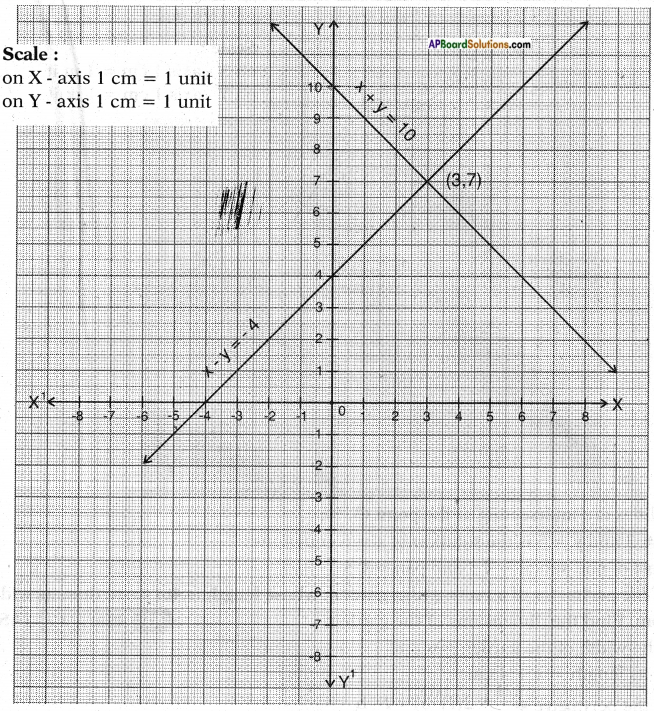
∴ Number of boys = 3 and the number of girls = 7

Question 5.
5 pencils and 7 pens together cost Rs. 50 whereas 7 pencils and 5 pens together cost Rs. 46. Find the cost of one pencil and that of one pen.
Answer:
Let the cost of each pencil be Rs. x
and the cost of each pen be Rs. y.
By problem 5x + 7y = 50
7x + 5y = 46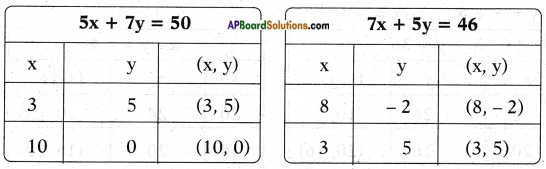

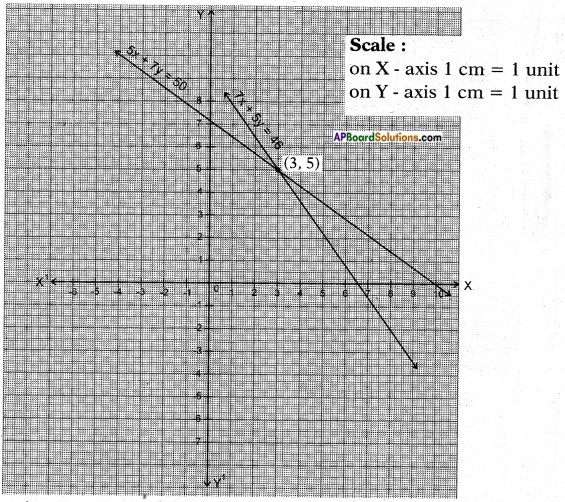
The lines are intersecting at the point (3, 5).
x = 3 and y = 5 is the solution of given equations.
∴ Cost of one pencil = Rs. 3 and pen = Rs. 5

Question 6.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width is 36 m. Find the dimensions of the garden.
Answer:
Let the width of the garden = x cm
then its length = x + 4 cm
Half the perimeter = 12 × 2(7+ b) = l + b
By problem, x + x + 4 = 36
2x + 4 = 36
2x = 36 – 4 = 32
∴ x = 16 and x + 4 = 16 + 4 = 20
i.e., length = 20 cm and breadth = 16 cm.
(or)
Let the breadth be x and length = y
then x + y = 36 ⇒ x + y = 36
y = x + 4 ⇒ x – y = -4

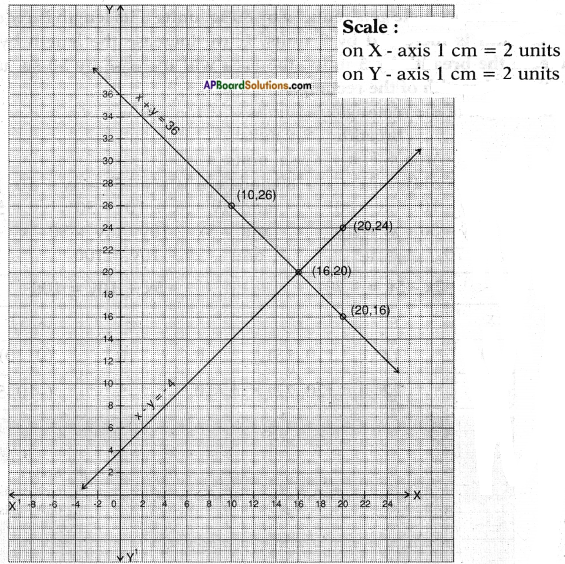
The two lines intersect at the point (16, 20)
i.e., length = 20 cm and the breadth = 16 cm.

Question 7.
We have a linear equation 2x + 3y – 8 = 0. Write another linear equation in two variables such that the geometrical representation of the pair so formed is intersect¬ing lines. Now, write two more linear equations so that one forms a pair of parallel lines and the second forms coincident line with the given equation.
Answer:
i) Given: 2x + 3y – 8 = 0
The lines are intersecting lines.
Let the other linear equation be ax + by + c = 0
∴ 𝑎1𝑎2 ≠ 𝑏1𝑏2; we have to choose appropriate values satisfying the condition above.
Thus the other equation may be 3x + 5y – 6 =0

ii) Parallel line 𝑎1𝑎2 = 𝑏1𝑏2 ≠ 𝑐1𝑐2
⇒ 2x + 3y – 8 = 0
4x + 6y – 10 = 0

iii) Coincident lines 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2
⇒ 2x + 3y – 8 = 0 ⇒ 8x + 12y – 32 = 0

Question 8.
The area of a rectangle gets reduced by 80 sq. units if its length is reduced by 5 units and breadth is increased by 2 units. If we increase the length by 10 units and decrease the breadth by 5 units, the area will increase by 50 sq. units. Find the length and breadth of the rectangle.
Answer:
Let the length of the rectangle = x units
breadth = y units Area = l . b = xy sq. units
By problem, (x – 5) (y + 2) = xy – 80 and (x + 10) (y – 5) = xy + 50
⇒ xy + 2x – 5y – 10 = xy – 80 and xy – 5x + 10y – 50 = xy + 50
⇒ 2x – 5y = xy – 80 – xy + 10 and -5x + 10y = xy + 50 – xy + 50
⇒ 2x – 5y = – 70 and -5x + 10y = 100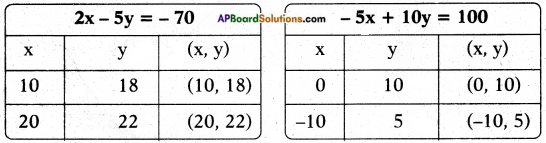

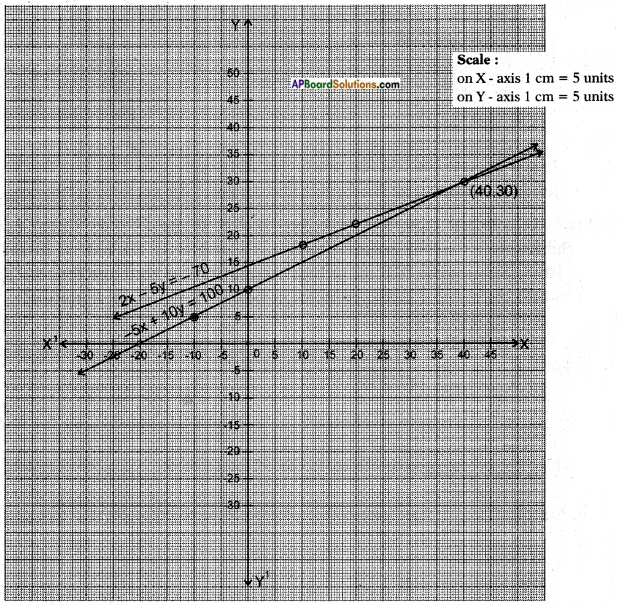
The two lines intersect at the point (40, 30)
∴ The solution is x = 40 and y = 30
i.e., length = 40 units; breadth = 30 units.

Question 9.
In X class, if three students sit on each bench, one student will be left. If four students sit on each bench, one bench will be left. Find the number of students and the number of benches in that class.
Answer:
Let the number of benches = x say and the number of students = y
By problem
y = 3x + 1 ⇒ 3x – y + 1 = 0
and y = 4(x – 1) ⇒ 4x – y – 4 = 0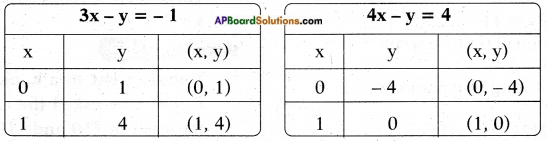

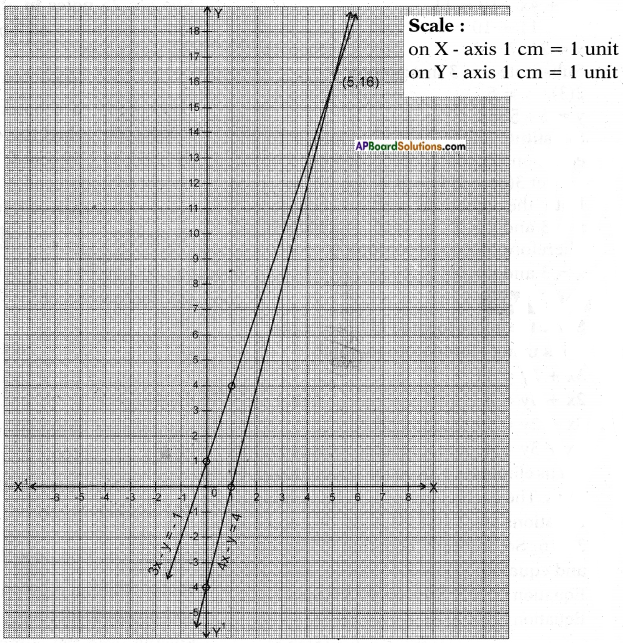
The two lines intersect at (5, 16)
∴ The solution of the equation is x = 5 and y = 16
i.e., Number of benches = 5 and the number of students = 16

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 exam preparation. The AP Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1, AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1, Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook solutions, AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1, AP Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1, Andhra Pradesh State Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook solutions, AP Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022