Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbooks Solutions PDF
Andhra Pradesh State Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 10th |
| Subject | Maths |
| Chapters | Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Answers.
- Look for your Andhra Pradesh Board STD 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions for PDF Free.
AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 10th Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables InText Questions and Answers
Question 1.
Solve the following systems of equations: i) x – 2y = 0; 3x + 4y = 20 (Page No. 79)
Answer:
i) x – 2y = 0; 3x + 4y = 20
-2y = -x 4y = 20 – 3x
y = 𝑥2 y = 20−3𝑥4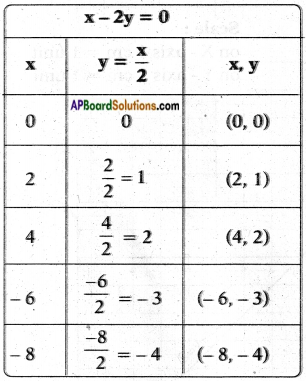

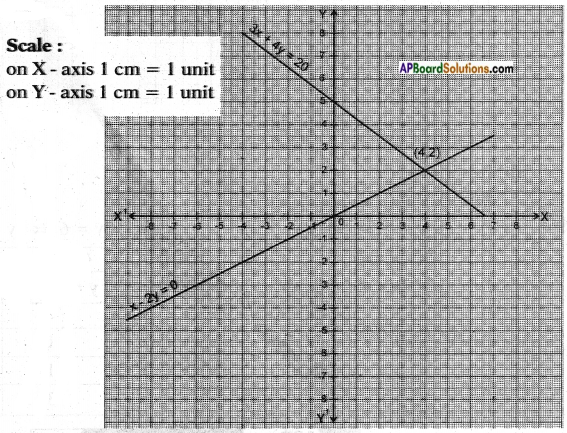
The two lines meet at (4, 2).
The solution set is {(4, 2)}
ii) x + y = 2
2x + 2y = 4
Answer:
x + y = 2
2x + 2y = 4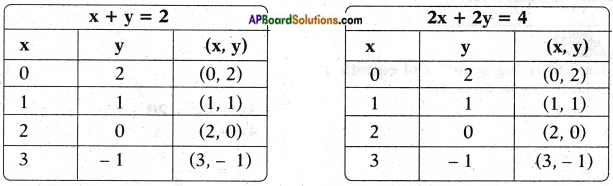
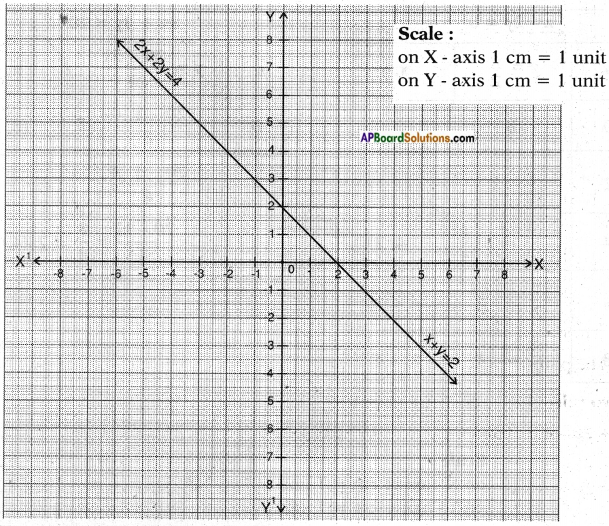
These two are coincident lines.
∴ There are infinitely many solutions.
iii) 2x – y = 4
4x – 2y = 6
Answer:
2x – y = 4 4x – 2y = 6
⇒ y = 2x – 4 ⇒ 2y = 4x – 6 ⇒ y = 2x – 3
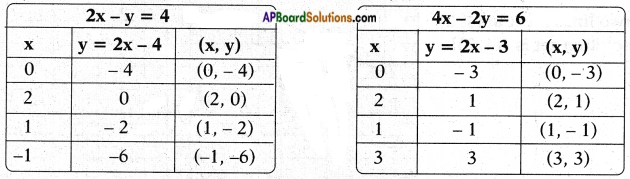
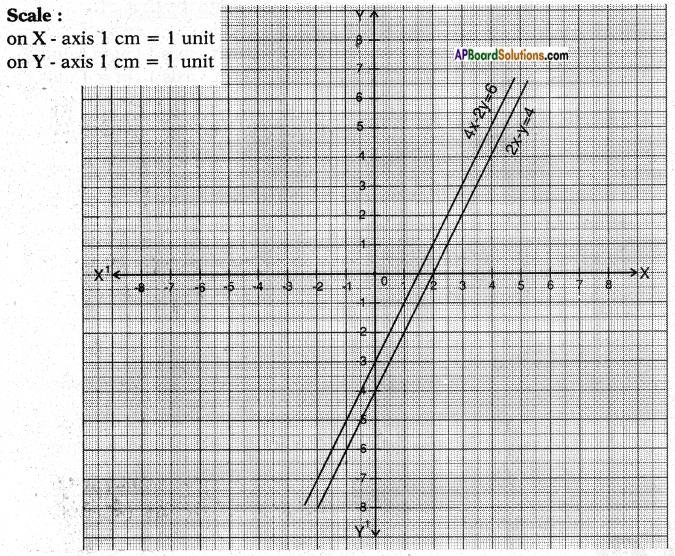
These two are parallel lines.
∴ The pair of linear equations has no solution.
Question 2.
Two rails of a railway track are represented by the equations.
x + 2y – 4 = 0 and 2x + 4y – 12 = 0. Represent this situation graphically. (Page No. 79)
Answer:
x + 2y – 4 = 0 2x + 4y – 12 = 0
2y = 4 – x 4y = 12 – 2x (or) 4y = 2 (6 – x)
y = 4−𝑥2 y = 6−𝑥2
x + 2y – 4 = 0 2x + 4y – 12 = 0
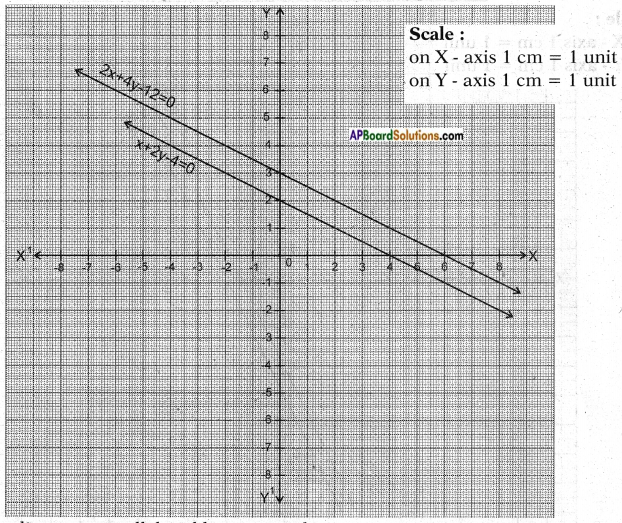
These lines are parallel and hence no solution.
Question 3.
Check each of the given systems of equations to see if it has a unique solution, infinitely many solutions or no solution. Solve them graphically. (Page No. 83)
i) 2x + 3y = 1
3x – y = 7
Answer:
Let a1x + b1y – c1 = 0 ≃ 2x + 3y – 1 = 0
a2x + b2y + c2 = 0 ≃ 3x – y – 7 = 0
Now comparing their coefficients i.e., 𝑎1𝑎2 and 𝑏1𝑏2
⇒ 23 ≠ 3−1
The given lines are intersecting lines.
2x + 3y = 1 3x – y = 7
3y = 1 – 2x y – 3x = 7
y = 1−2𝑥3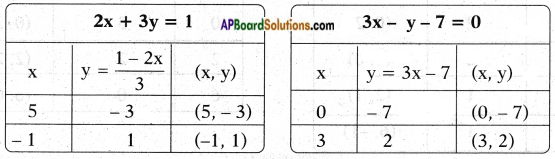
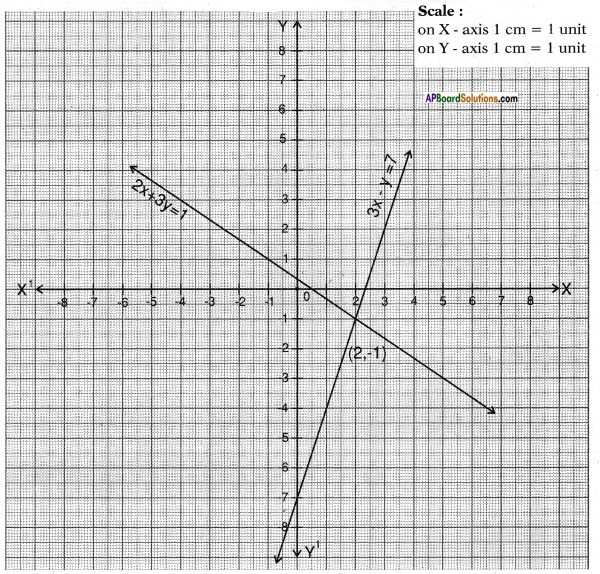
The system of equations has a unique solution (2, – 1).
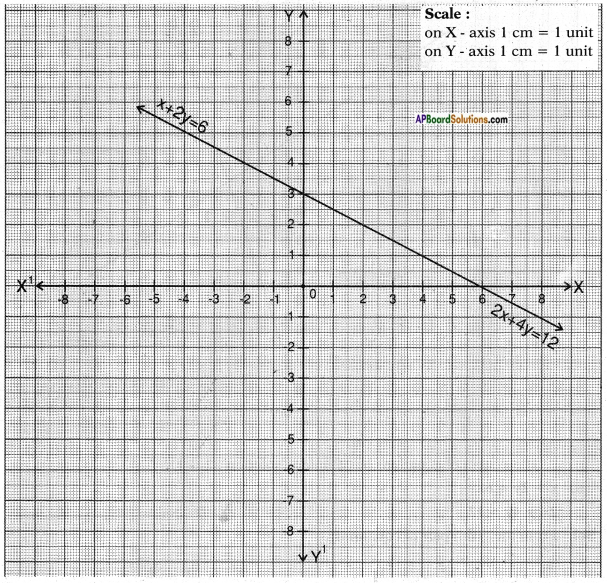
ii) x + 2y = 6
2x + 4y = 12
Answer:
From the given pair of equations,
𝑎1𝑎2 = 12;
𝑏1𝑏2 = 24 = 12;
𝑐1𝑐2 = 612 = 12
∴ 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2
∴ The lines are dependent and have infinitely many solutions.
x + 2y = 6 2x + 4y = 12
2y = 6 – x 4y = 12 – 2x (or) 4y = 2(6 – x)
y = 6−𝑥2 y = 12−2𝑥4 or y = 6−𝑥2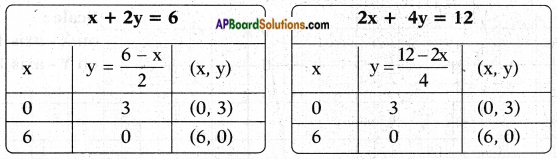
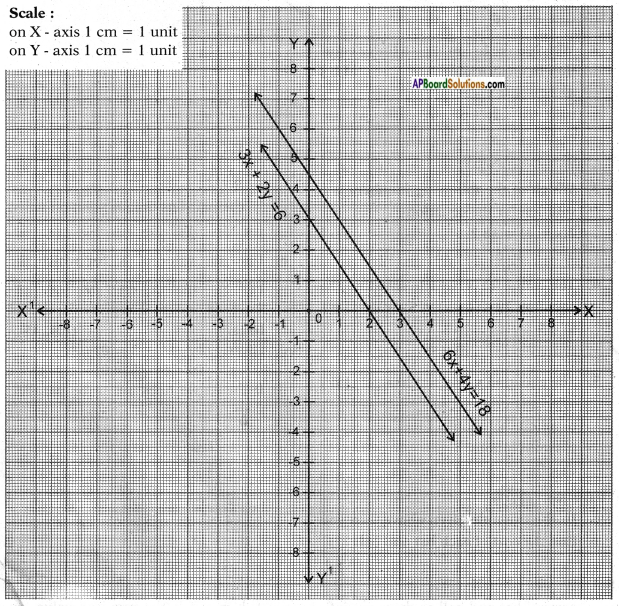
iii) 3x + 2y = 6
6x + 4y = 18
Answer:
From the given pair of equations,
𝑎1𝑎2 = 36 = 12;
𝑏1𝑏2 = 24 = 12;
𝑐1𝑐2 = 618 = 13
∴ 𝑎1𝑎2 = 𝑏1𝑏2
∴ The lines are parallel and hence no solution.
3x + 2y = 6 6x + 4y = 18
2y = 6 – 3x 4y = 18 – 6x
y = 6−3𝑥2 y = 18−6𝑥4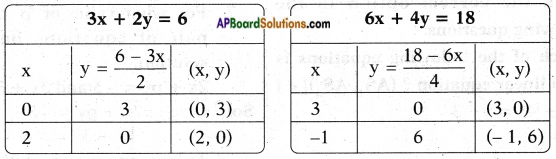
Try these
(Page No. 75, 76)
Question 1.
Mark the correct option in the following questions:
Which of the following equations is not a linear equation?
a) 5 + 4x = y + 3
b) x + 2y = y – x
c) 3 – x = y2 + 4
d) x + y = 0
Answer:
[ c ]
Question 2.
Which of the following is a linear equation in one variable?
a) 2x + 1 = y – 3
b) 2t – 1= 2t + 5
c) 2x – 1 = x2
d) x2 – x + 1 =0
Answer:
[ b ]
Question 3.
Which of the following numbers is a solution for the equation 2(x + 3) = 18?
a) 5
b) 6
c) 13
d) 21
Answer:
[b]
Question 4.
The value of x which satisfies the equation 2x – (4 – x) = 5 – x is
a) 4.5
b) 3
c) 2.25
d) 0.5
Answer:
[ c ]
Question 5.
The equation x – 4y = 5 has
a) no solution
b) unique solution
c) two solutions
d) infinitely many solutions
Answer:
[ d ]
Question 6.
In the example given above, can you find the cost of each bat and ball? (Page No. 79)
Answer:
We can’t find the exact values for the costs of bat and ball as there are infinitely many possibilities.
Question 7.
For what value of ‘p’ the following pair of equations has a unique solution. (Page No. 83)
2x + py = – 5 and 3x + 3y = – 6
Answer:
Given: 2x + py = – 5
3x 4- 3y = – 6
To have an unique solution we should have
∴ The pair has unique solution when p ≠ 2.
Question 8.
Find the value of ‘k’ for which the pair of equations 2x – ky + 3 = 0, 4x + 6y – 5 = 0 represent parallel lines. (Page No. 83)
Answer:
Given: 2x – ky + 3 = 0
4x + 6y – 5 = 0
If the above lines are to be parallel, then
∴ k = – 3 is the required value for which lines are parallel.
Question 9.
For what value of ‘k’, the pair of equation 3x + 4y + 2 = 0 and 9x + 12y + k = 0 represent coincident lines. (Page No. 83)
Answer:
Given: 3x + 4y + 2 = 0
9x + 12y + k = 0
If the lines are to be coincident with each other, then
∴ k = 2 × 3 = 6
Question 10.
For what positive values of ‘p’ the following pair of linear equations have infinitely many solutions? (Page No. 83)
px + 3y – (p – 3) = 0
12x + py – p = 0
Answer:
Given: px + 3y – (p – 3) = 0
12x + py – p = 0
The above equations to have infinitely many solutions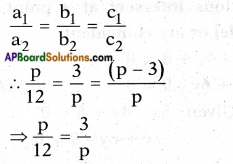
p.p = 12 × 3
⇒ p2 = 36
⇒ p = ±6
Think & Discuss
Question 1.
Two situations are given below:
i) The cost of 1 kg potatoes and 2 kg tomatoes was Rs. 30 on a certain day. After two days, the cost of 2 kg potatoes and 4 kg tomatoes was found to be Rs. 66.
ii) The coach of a cricket team of M.K. Nagar High School buys 3 bats and 6 balls for Rs. 3900. Later he buys one more bat and 2 balls for Rs. 1300.
Identify the unknowns in each situation. We observe that there are two unknowns in each case. (Page No. 73)
Answer:
i) The unknowns in the first problem are
a) cost of 1 kg tomatoes
b) cost of 1 kg potatoes
ii) In the second problem, the unknowns are
a) cost of each bat
b) cost of each ball
Question 2.
Is a dependent pair of linear equations always consistent? Why or why not? (Page No. 79)
Answer:
Reason: 𝑎1𝑎2 = 𝑏1𝑏2 = 𝑐1𝑐2 always holds. In other words, they have infinitely many solutions.
Do these
Solve each pair of equations by using the substitution method. (Page No. 88)
Question 1.
3x – 5y = -1
x – y = -1
Answer:
Given: 3x – 5y = -1 ……. (1)
x – y = -1 …….. (2)
From equation (2), x – y = – 1
x = y – 1
Substituting x = y – 1 in equation (1)
we get
3 (y – 1) – 5y = – 1
⇒ 3y – 3 – 5y = r 1
⇒ – 2y = – 1 + 3
⇒ 2y = – 2
⇒ y = -1
Substituting y = – 1 in equation (1) we get
3x – 5 (- 1) = -1
3x + 5 = – 1
3x = – 1 – 5
x = −63 = -2
∴ The solution is (-2, -1)
Question 2.
x + 2y = – 1
2x – 3y = 12
Answer:
Given: x + 2y = -1 ……. (1)
2x – 3y = 12 …….. (2)
From equation (1)x + 2y = -l
⇒ x = – 1 – 2y
Substituting x = – 1 – 2y in equation (2), we get
2 (- 1 – 2y) – 3y = 12
– 2 – 4y – 3y = 12
– 2 – 7y = 12
7y = – 2 – 12
∴ y = −147 = -2
Substituting y = – 2 in equation (1), we get
x + 2 (- 2) = – 1
x = – 1 + 4
x = 3
∴ The solution is (3, – 2)
Question 3.
2x + 3y = 9
3x + 4y = 5
Answer:
Given: 2x + 3y – 9 …….. (1)
3x + 4y = 5 ……. (2)
From equation (1);
2x = 9 – 3y
x = 9−3𝑦2
Substituting x = 9−3𝑦2 in equation (2)
we get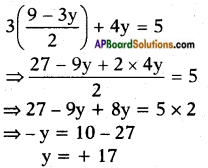
Substituting y = + 17 in equation (1) we get
2x + 3 (+ 17) = 9
⇒ 2x = 9 – 51
⇒ 2x = -42
⇒ x = -21
∴ The solution is (-21, 17)
Question 4.
x + 6𝑦 = 6
3x – 8𝑦 = 5
Answer:
Given:
x + 6𝑦 = 6 …….. (1)
3x – 8𝑦 = 5 …….. (2)
From equation (1) x = 6 – 6𝑦
Substituting x = 6 – 6𝑦 in equation (2)
we get
Substituting y = 2 in equation (1) we get
x + 62 = 6 ⇒ x + 3 = 6
∴ x = 3
∴ The solution is (3, 2)
Question 5.
0.2x + 0.3y =1.3
0.4x + 0.5y = 2.3
Answer:
Given:
0.2x + 0.3y = 1.3
⇒ 2x + 3y = 13 …… (1)
0.4x + 0.5y = 2.3
⇒ 4x + 5y = 23 …… (2)
From equation (1)
2x = 13 – 3y
⇒ x = 13−3𝑦2
Substituting x = 13−3𝑦2 equation (2) we get
13−3𝑦2 + 5y = 23
⇒ 26 – 6y + 5y = 23
⇒ -y + 26 = 23
⇒ y = 26 — 23 = 3
Substituting y = 3 in equaion (1) we get
2x + 3(3) = 13
⇒ 2x + 9 = 13
⇒ 2x = 13 – 9
⇒ 2x = 4
⇒ x = 42 = 2
∴ The solution is (2, 3)
Question 6.
√2x + √3y = 0
√3x – √8y = 0
Answer:
Given:
√2x + √3y = 0 ……. (1)
√3x – √8y = 0 ……. (2)
Substitute x = 0 in (1),
√2(0) + √3y = 0
√3y = 0
∴ y = 0
∴ The solution is x = 0, y = 0
Note: a1x + b1y + c1 = 0
a2x + b2y + c2 = 0, if c1 = c2 = 0
then, x = 0, y = 0 is a solution.
Solve each of the following pairs of equations by the elimination method. (Page No. 89)
Question 7.
8x + 5y = 9
3x + 2y = 4
Answer:
Given: 8x + 5y = 9 ……. (1)
3x + 2y = 4 …….. (2)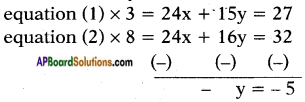
∴ y = 5
Substituting y = 5 in equation (1) we get
8x + 5 × 5 = 9
⇒ 8x = 9 – 25
x = −168 = -2
∴ The solution is (- 2, 5)
Question 8.
2x + 3y = 8
4x + 6y = 7
Answer:
Given: 2x + 3y = 8 ……. (1)
4x + 6y = 7 …….. (2)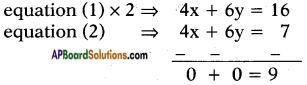
The lines are parallel.
∴ The pair of lines has no solution.
Question 9.
3x + 4y = 25
5x – 6y = -9
Answer:
Given: 3x + 4y = 25 ……. (1)
5x – 6y = -9 …….. (2)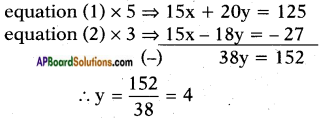
Substituting y = 4 in equation (1) we get
3x + 4 × 4 = 25
3x = 25 – 16
⇒ x = 93 = 3
∴ (3,4) is the solution for given pair of lines.
Question 10.
In a competitive exam, 3 marks are awarded for every correct answer and for every wrong answer, 1 mark will be deducted. Madhu scored 40 marks in this exam. Had 4 marks been awarded for each correct answer and 2 marks deducted for each incorrect answer, Madhu would have scored 50 marks. How many questions were there in the test? (Madhu attempted all the questions) .
Now use the elimination method to solve the above example – 9.
Answer:
The equations formed are
3x – y = 40 ……. (1)
4x – 2y = 50 …….. (2)
Substituting y = 5 in equation (1) we get
3x – 5 = 40
⇒ 3x = 40 + 5
⇒ x = 453 = 15
Total number of questions = Number of correct questions + Number of wrong answers
= x + y
= 15 + 5 = 20
Question 11.
Mary told her daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Find the present age of Mary and her daughter. Solve example – 10 by the substitution method.
Answer:
The equations formed are
The equations formed are
x – 7y + 42 = 0 ……. (1)
x – 3y – 6 = 0 …….. (2)
From (1), x = – 42 + 7y
Substituting x = – 42 + 7y in equation (2) we get
-42 + 7y – 3y – 6 = 0
⇒ 4y – 48 = 0
⇒ y = 484 = 12
Substituting y = 12 in equation (2) we get
x – 3 × 12 – 6 = 0
x – 36 – 6 = 0
x = 42
Try this
Question 1.
Solve the given pair of linear equations, (a – b)x + (a + b)y = a2 – 2ab – b2
(a + b) (x + y) = a2 + b2 (Page No. 89)
Answer: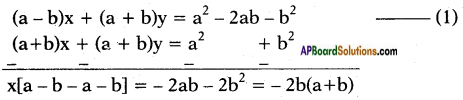
x(-2b) = – 2b(a + b)
⇒ x = (a + b)
Put this value of ‘x’ in eq (1) we get
(a – b) (a + b) + (a + b)y = a2 – 2ab – b2
a2 – b2 + (a + b)y = a2 – 2ab – b2
⇒ y = −2𝑎𝑏𝑎+𝑏
∴ Solution to given pair of linear equations x = a + b, y = −2𝑎𝑏𝑎+𝑏
AP Board Textbook Solutions PDF for Class 10th Maths
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF








0 Comments:
Post a Comment