AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Book Answers

AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 11 Trigonometry Ex 11.1
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 11th Lesson Trigonometry Ex 11.1 Textbook Questions and Answers

Question 1.
In right angle triangle ABC, 8 cm, 15 cm and 17 cm are the lengths of AB, BC and CA respectively. Then, find out sin A, cos A and tan A.
Answer:
Given that
△ABC is a right angle triangle and Lengths of AB, BC and CA are 8 cm, 15 cm and 17 cm respectively.
Among the given lengths CA is longest.
Hence CA is the hypotenuse in △ABC and its opposite vertex having right angle.
i.e., ∠B = 90°.
With reference to ∠A, we have opposite side = BC = 15 cm
adjacent side = AB = 8 cm
and hypotenuse = AC = 17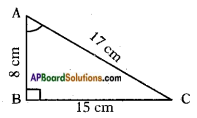

sin A = Opposite side of ∠A Hypotenuse = 𝐵𝐶𝐴𝐶 = 1517
cos A = Adjacent side of ∠A Hypotenuse = 𝐴𝐵𝐴𝐶 = 817
tan A = Opposite side of ∠A Adjacent side of ∠A = 𝐵𝐶𝐴𝐵 = 158
∴ sin A = 1517;
cos A = 817
tan A = 158

Question 2.
The sides of a right angle triangle PQR are PQ = 7 cm, QR = 25 cm and ∠P = 90° respectively. Then find, tan Q – tan R.
Answer: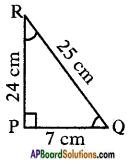

Given that △PQR is a right angled triangle and PQ = 7 cm, QR = 25 cm.
By Pythagoras theorem QR² = PQ² + PR²
(25)² = (7)² + PR²
PR² = (25)² – (7)² = 625 – 49 = 576
PR = √576 = 24 cm
tan Q = 𝑃𝑅𝑃𝑄 = 247;
tan R = 𝑃𝑄𝑃𝑅 = 724
∴ tan Q – tan R = 247 – 724
= (24)2−(7)2168
= 576−49168
= 527168

Question 3.
In a right angle triangle ABC with right angle at B, in which a = 24 units, b = 25 units and ∠BAC = θ. Then, find cos θ and tan θ.
Answer:
Given that ABC is a right angle triangle with right angle at B, and BC = a = 24 units, CA = b = 25 units and ∠BAC = θ.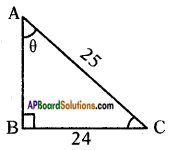

By Pythagoras theorem
AC² = AB² + BC²
(25)² = AB² + (24)²
AB² = 25² – 24² = 625 – 576
AB² = 49
AB = √49 = 1
With reference to ∠BAC = θ, we have
Opposite side to θ = BC = 24 units.
Adjacent side to θ = AB = 7 units.
Hypotenuse = AC = 25 units.
Now
cos θ = Adjacent side of 𝜃 Hypotenuse = 𝐴𝐵𝐴𝐶 = 725
tan θ = Opposite side of 𝜃 Adjacent side of 𝜃 = 𝐵𝐶𝐴𝐵 = 247
Hence cos θ = 725 and tan θ = 247

Question 4.
If cos A = 1213, then find sin A and tan A.
Answer:
From the identity
sin² A + cos² A = 1
⇒ sin² A = 1 – cos² A
= 1 – (1213)2
= 1 – 144169
= 169−144169
= 25169
∴ sin A = 25169‾‾‾‾√ = 513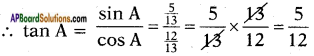

∴ sin A = 513; tan A = 512

Question 5.
If 3 tan A = 4, then find sin A and cos A.
Answer:
Given 3 tan A = 4
⇒ tan A = 43
From the identify sec² A – tan² A = 1
⇒ 1 + tan² A = sec² A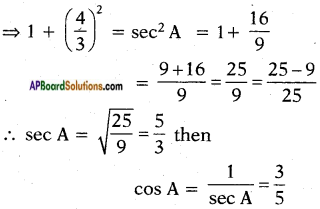

If cos A = 35 then from
sin² A + cos² A = 1
We can write sin²A = 1 – cos²A
= 1 – (35)2
= 1 – 925
⇒ sin² A = 1625
⇒ sin A = 45
∴ sin A = 45; cos A = 35

Question 6.
In △ABC and △XYZ, if ∠A and ∠X are acute angles such that cos A = cos X then show that ∠A = ∠X.
Answer: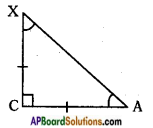

In the given triangle, cos A = cos X
⇒ 𝐴𝐶𝐴𝑋 = 𝑋𝐶𝐴𝑋
⇒ AC = XC
⇒ ∠A = ∠X (∵ Angles opposite to equal sides are also equal)

Question 7.
Given cot θ = 78, then evaluate

Answer: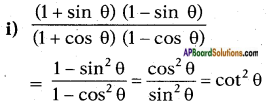

cot² θ = (cot θ)²
= (78)2 = 4964 …… (1)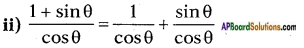

= sec θ + tan θ
So cot θ = 78
⇒ tan θ = 87
⇒ tan² θ = (87)2 = 6449
From sec² θ – tan² θ = 1
⇒ 1 + tan² θ = sec² θ

Question 8.
In a right angle triangle ABC, right angle is at B, if tan A = √3, then find the value of
i) sin A cos C + cos A sin C
ii) cos A cos C – sin A sin C
Answer:
Given, tan A = 3√1
Hence Opposite side Adjacent side =3√1
Let opposite side = √3k and adjacent side = 1k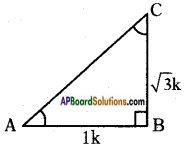

In right angled △ABC,
AC² = AB² + BC²
(By Pythagoras theorem)
⇒ AC² = (1k)² + (√3k)²
⇒ AC² = 1k² + 3k²
⇒ AC² = 4k²
∴ AC = 4𝑘2‾‾‾‾√ = 2k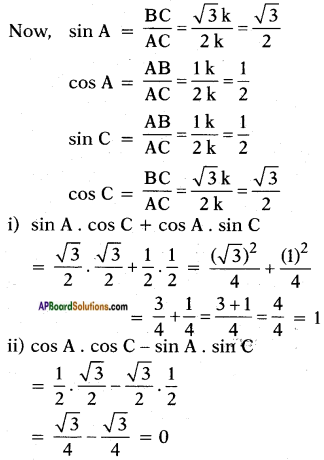

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 exam preparation. The AP Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1, AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1, Andhra Pradesh State Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook solutions, AP Board Class 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1, AP Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1, Andhra Pradesh State Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbook solutions, AP Board STD 10th Maths Chapter 11 Trigonometry Ex 11.1 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022