 |
| AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 3 Polynomials InText Questions Book Answers |
Andhra Pradesh Board Class 10th Maths Chapter 3 Polynomials InText Questions Textbooks Solutions PDF
Andhra Pradesh State Board STD 10th Maths Chapter 3 Polynomials InText Questions Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 3 Polynomials InText Questions Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 3 Polynomials InText Questions solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 3 Polynomials InText Questions Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 3 Polynomials InText Questions Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.Andhra Pradesh State Board Class 10th Maths Chapter 3 Polynomials InText Questions Books Solutions
| Board | AP Board |
| Materials | Textbook Solutions/Guide |
| Format | DOC/PDF |
| Class | 10th |
| Subject | Maths |
| Chapters | Maths Chapter 3 Polynomials InText Questions |
| Provider | Hsslive |
How to download Andhra Pradesh Board Class 10th Maths Chapter 3 Polynomials InText Questions Textbook Solutions Answers PDF Online?
- Visit our website - Hsslive
- Click on the Andhra Pradesh Board Class 10th Maths Chapter 3 Polynomials InText Questions Answers.
- Look for your Andhra Pradesh Board STD 10th Maths Chapter 3 Polynomials InText Questions Textbooks PDF.
- Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 3 Polynomials InText Questions Textbook Solutions for PDF Free.
AP Board Class 10th Maths Chapter 3 Polynomials InText Questions Textbooks Solutions with Answer PDF Download
Find below the list of all AP Board Class 10th Maths Chapter 3 Polynomials InText Questions Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:10th Class Maths 3rd Lesson Polynomials InText Questions and Answers
Do these
Question 1.
State which of the following are polynomials and which are not? Give reasons. (Page No. 48)
(i) 2x3
(ii) 1𝑥−1
(iii) 4z2 + 17
(iv) m2 – √2 m + 2
(v) p-2 + 1
Answer:
i) 2x3 is a polynomial.
ii) 1𝑥−1 is not a polynomial because its power is negative integer exponent.
iii) 4z2 + 17 is a polynomial.
iv) m2 – √2 m + 2 is a polynomial.
v) p-2 + 1 is not a polynomial because its power is negative integer exponent.
Question 2.
p(x) = x2 – 5x – 6, find the values of p(l), p(2), p(3), p(0), p(-l), p(-2), p(-3). (Page No. 49)
Answer:
Given polynomial p(x) = x2 – 5x – 6
p(1) = (1)2 – 5(1) – 6 = 1 – 5 – 6 = – 10
p(2) = (2)2 – 5(2) – 6 = 4 – 10 – 6 = -12
p(3) = 32 – 5(3) – 6 = 9 – 15 – 6 = – 12
p(0) = 02 – 5(0) – 6 = – 6
p(-1) = (-1)2 – 5(-1) – 6 = 1 + 5 – 6 = 0
p(-2) = (-2)2 – 5(-2) – 6 = 4 + 10 – 6 = 8
p(-3) = (-3)2 – 5(-3) – 6 = 9 + 15 – 6 = 18
Question 3.
p(m) = m2 – 3m + 1, find the values of p(1)and p(-1). (Page No. 49)
Answer:
Given polynomial p(m) = m2 – 3m + 1
p(1) = (1)2 – 3(1) + 1 = 1 – 3 + 1 = 2 – 3 = – 1
p(-1) = (-1)2 – 3(-1) + 1 = 1 + 3 + 1 = 5
Question 4.
Let p(x) = x2 – 4x + 3. Find the values of p(0), p(l), p(2), p(3) and obtain zeroes of the polynomial p(x). (Page No. 50)
Answer:
Given polynomial p(x) = x2 – 4x + 3
p(0) = (0)2 – 4(0) + 3 = 3
p(1) = (1)2 – 4(1) + 3 = 1 – 4 + 3 = 0
p(2) = (2)2 – 4(2) + 3 = 4 – 8 + 3 = – 1
p(3) = (3)2 – 4(3) + 3 = 9 – 12 + 3 = 0
We see that p(1) and p(3) are zeroes of the polynomial p(x).
Question 5.
Check whether -3 and 3 are the zeroes of the polynomial x2 – 9. (Page No. 50)
Answer:
Given polynomial p(x) = x2 – 9
Zero of the polynomial p(x) = 0
x2 – 9 = 0
⇒ x2 = 9
⇒ x = V9 = ± 3
∴ x = + 3, – 3
∴ Zeroes of the polynomial p(x) are – 3 and 3.
Try these
Question 1.
Write 3 different quadratic, cubic and 2 linear polynomials with different number of terms. (Page No. 48)
Answer:
Quadratic polynomials: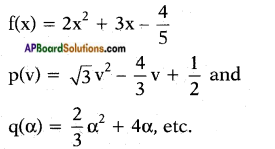
Cubic polynomials :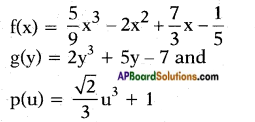
Linear polynomials :
f(t) = √2 t + 5
g(u) = 23 u – 52 and
q(y) = 3y
Yes, we can write polynomials of any degree.
Question 2.
Write a quadratic polynomial and a cubic polynomial in variable x in the general form. (Page No. 49)
Answer:
General form of a quadratic polynomial having variable ‘x’ is
f(x) = ax3 + bx2 + c, a ≠ 0
General form of a cubic polynomial having variable ‘x’ is
f(x) = ax3 + bx2 + cx + d, a ≠ 0
Question 3.
Write a general polynomial q(z) of degree n with coefficients that are b0…. bn. What are the conditions on b0…. bn. (Page No. 49)
Answer:
q(z) = b0zn + b1zn-1 + b2zn-2 …….. + bn-1z + bn is a polynomial of n degree where b0, b1, b2,…… bn-1, bn are real coefficients and b0 ≠ 0.
Do this
Question 1.
Draw the graph of i) y = 2x + 5, ii) y = 2x – 5, iii) y = 2x and find the point of intersection on X – axis. Is the x-coordinates of these points also the zero of the polynomial? (Page No. 52)
Answer:
i) Given that y = 2x + 5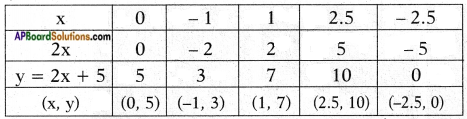
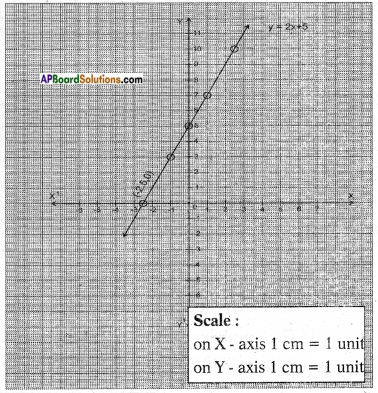
Result: The graph y = 2x + 5 cuts the X – axis at the point (-2.5, 0).
Hence, the zeroes of the polynomial is -2.5.
ii) Given that y = 2x – 5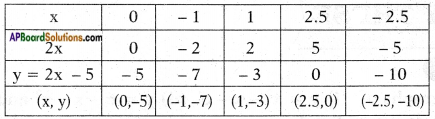
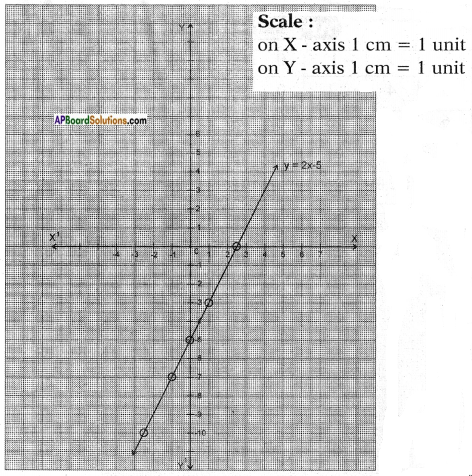
Result: The graph of y = 2x – 5 cuts the X – axis at the point (2.5, 0).
The zeroes of the polynomial is 2.5 = 52
iii) Given that y = 2x
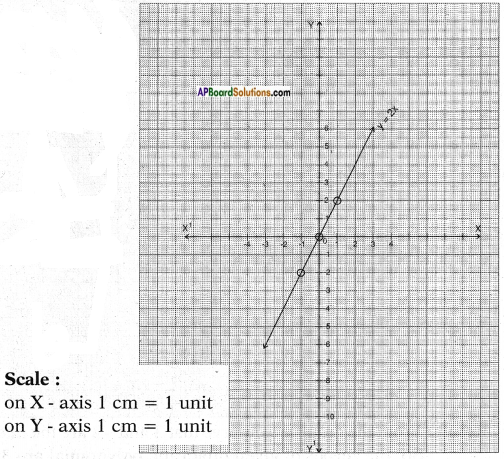
Result: The graph passes through the origin.
So, the zeroes of the polynomial y = 2x is zero.
Try these
Question 1.
Draw the graphs of (i) y = x2 – x – 6 (ii) y = 6 – x – x2 and find zeroes in each case. What do you notice? (Page No. 53)
Answer:
i) Given that y = x2 – x – 6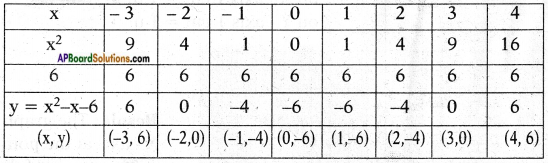
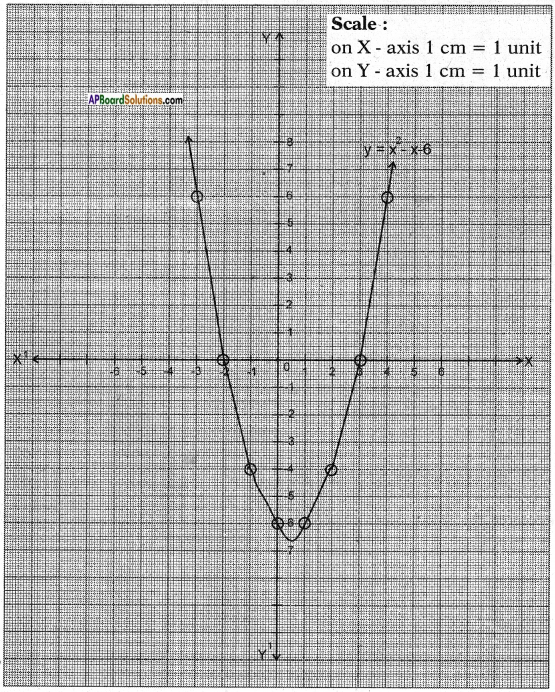
Result: From the graph we observe that 3 and -2 are the intersecting points of X – axis.
So, the zeroes of given quadratic polynomial are 3 and -2.
ii) Given that y = 6 – x – x2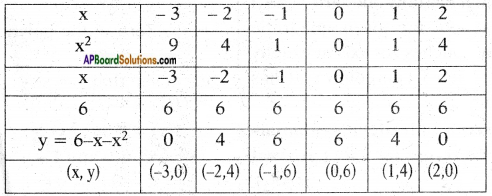
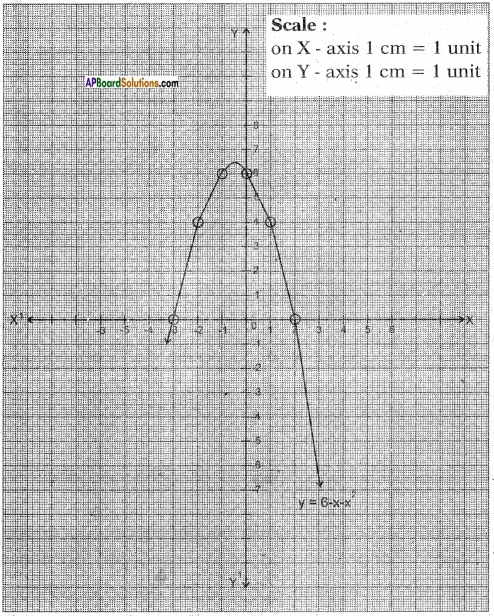
Result: From the graph we observe that – 3 and 2 are the intersecting points ol X – axis.
So, the zeroes of given quadratic polynomial are – 3 and 2.
Question 2.
Write three quadratic polynomials that have 2 zeroes each. (Page No. 55)
Answer:
y = x2 – x – 2 having two zeroes, i.e., (2, 0) and (- 1, 0).
y = 3 – 2x – x2 having two zeroes i.e., (1,0) and (- 3, 0).
y = x2 – 3x – 4 having two zeroes i.e., (-1, 0) and (4, 0)
Question 3.
Write one quadratic polynomial that has one zero. (Page No. 55)
Answer:
Quadratic Polynomial y = x2 – 6x + 9 has only one zero i.e., 3.
Question 4.
How will you verify if a quadratic polynomial it has only one zero? (Page No. 55)
Answer:
If the graph of the given quadratic polynomial touches X – axis at exactly one point, then I can confirm it has only one zero.
Question 5.
Write three quadratic polynomials that have no zeroes for x that are real numbers. (Page No. 55)
Answer:
The quadratic polynomials y = 2x2 – 4x + 5 and y = – 3x2 + 2x – 1 and y = x2 – 2x + 4 have no zeroes.
Question 6.
Find the zeroes of cubic polynomials
(i) – x3
(ii) x2 – x3
(iii) x3 – 5x2 + 6x
without drawing the graph of the polynomial. (Page No. 57)
Answer:
i) Given polynomial is y = – x3
f(x) = -x3 ; f(x) = 0
x3 = 0
x = 0‾√3 = 0
∴ Zero of the polynomial f(x) is only one i.e., 0.
ii) Given that y = x2 – x3
f(x) = x2 (1 – x)
f(x) = 0
⇒ x2 (1 – x) = 0
⇒ x2 = 0 and 1 – x = 0
⇒ x = 0 and x = 1
∴ The zeroes of the polynomial f(x) are two i.e., 0 and 1.
iii) Given that x3 – 5x2 + 6x Let f(x) = x3 – 5x2 + 6x
= x(x2 – 5x + 6)
= x(x2 – 2x – 3x + 6)
= x[x(x – 2) – 3(x – 2)]
= x(x – 2) (x – 3)
∴ The zeroes of the polynomial f(x) are x = 0 and x = 2 and x = 3
Do these
Question 1.
Find the zeroes of the quadratic polynomials given below. Find the sum and product of the zeroes and verify relationship to the coefficients of terms in the polynomial. (Page No. 62)
i) p(x) = x2 – x – 6
ii) p(x) = x2 – 4x + 3
iii) p(x) = x2 – 4
iv) p(x) = x2 + 2x + 1
Answer:
i) Given polynomial p(x) = x2 – x – 6
We have x2 – x – 6 = x2 – 3x + 2x – 6
= x(x – 3) + 2(x – 3)
= (x – 3) (x + 2)
So, the value of x2 – x – 6 is zero when x – 3 = 0 or x + 2 = 0
i.e., x = 3 or x = -2
So, the zeroes of x2 – x – 6 are 3 and – 2.
∴ Sum of the zeroes = 3 – 2 = 1
= – Coefficient of 𝑥 Coefficient of 𝑥2 = −(−1)1 = 1
And product of the zeroes = 3 × (-2) = -6
= Constant term Coefficient of 𝑥2 = −61 = -6
ii) p(x) = x2 – 4x + 3
Answer:
Given polynomial p(x) = x2 – 4x + 3
We have, x2 – 4x + 3 = x2 – 3x – x + 3
= x(x – 3) – 1 (x – 3)
= (x – 3) (x – 1)
So, the value of x2 – 4x + 3 is zero when x – 3 = 0 or x – 1 =0, i.e.,
when x = 3 or x = 1 So, the zeroes of x2 – 4x + 3 are 3 and 1
∴ Sum of the zeroes = 3 + 1 = 4
= – Coefficient of 𝑥 Coefficient of 𝑥2 = −(−4)1 = 4
And product of the zeroes = 3 × 1 = 3
= Constant term Coefficient of 𝑥2 = 31 = 3
iii) Given polynomial p(x) = x2 – 4
We have, x2 – 4 = (x – 2) (x + 2)
So, the value of x2 – 4 is zero
when x – 2 = 0 or x + 2 = 0
i.e., x = 2 or x = – 2
So the zeroes of x2 – 4 are 2 and – 2
∴ Sum of the zeroes = 2 + (- 2) = 0
= – Coefficient of 𝑥 Coefficient of 𝑥2 = −01 = 0
And product of the zeroes = 2 × (-2) = -4
= Constant term Coefficient of 𝑥2 = −41 = -4
iv) Given polynomial p(x) = x2 + 2x + 1
We have x2 + 2x + 1 = x2 + x + x + 1
= x(x + 1) + l(x + 1)
= (x + 1) (x + 1)
So, the value of x2 + 2x + 1 is zero
when x + 1 = 0 (or) x + 1 = 0, i.e.,
when x = – 1 or – 1
o, the zeroes of x2 + 2x + 1 are – 1 and – 1.
∴ Sum of the zeroes = (-1) + (-1) = -2
= – Coefficient of 𝑥 Coefficient of 𝑥2 = −21 = -2
And product of the zeroes = (-1) × (-1) = 1
= Constant term Coefficient of 𝑥2 = 11 = 1
Question 2.
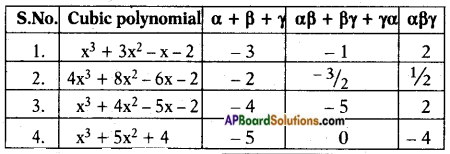
If α, β and γ are the zeroes of the given cubic polynomials, find the values as given in the table. (Page No. 66)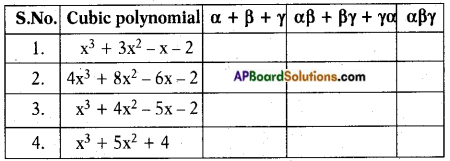
Answer:
l) Given polynomial is x3 + 3x2 – x – 2.
Comparing given polynomial with ax3 + bx2 + cx + d,
the values are a = 1, b = 3, c = -l, d = -2
α + β + γ = −𝑏𝑎 = −31 = -3
αβ + βγ + γα = 𝑐𝑎 = −11 = -1
αβγ = −𝑑𝑎 = −(−2)1 = 2
2) Given polynomial is 4x3 + 8x2 – 6x – 2
Compare the polynomial with ax3 + bx2 + cx + d = 0
Then a = 4, b = 8, c = – 6 and d = – 2
α + β + γ = −𝑏𝑎 = −84 = -2
αβ + βγ + γα = 𝑐𝑎 = −64 = −32
αβγ = −𝑑𝑎 = −(−2)4 = 12
3) Given polynomial is x3 + 4x2 – 5x – 2
Compare the polynomial with ax3 + bx2 + cx + d = 0
Then a = 1, b = 4, c = – 5 and d = – 2
α + β + γ = −𝑏𝑎 = −41 = -4
αβ + βγ + γα = 𝑐𝑎 = −51 = -5
αβγ = −𝑑𝑎 = −(−2)1 = 2
4) Given polynomial is x3 + 5x2 + 4
Compare the polynomial with ax3 + bx2 + cx + d = 0
Then a = 1, b = 5, c = 0 and d = 4
α + β + γ = −𝑏𝑎 = −51 = -5
αβ + βγ + γα = 𝑐𝑎 = 01 = 0
αβγ = −𝑑𝑎 = −41 = -4
Try this
Question 1.
i) Find a quadratic polynomial with zeroes -2 and 13. (Page No. 64)
Answer:
Let the quadratic polynomial be ax2 + bx + c, a ≠ 0 and its zeroes be α and β.
Here α = – 2 and β = 13
Sum of the zeroes = α + β
= -2 + 13 = −53
Product of the zeroes = αβ
= 13 × (-2) = −23
∴ ax2 + bx + c is [x2 – (α + β)x + αβ]
= [x2 – (−53)x + (−23)]
the quadratic polynomial will be 3x2 + 5x – 2.
ii) What is the quadratic polynomial whose sum of zeroes is −32 and the product of zeroes is -1.
Answer:
Let the quadratic polynomial be ax2 + bx + c and its zeroes be α and β.
Here α + β = −32 and αβ = -1
Thus, the polynomial formed = x2 – (α + β)x + αβ
= x2 – (−32)x + (-1)
= x2 + 3𝑥2 – 1
The other polynomials are (x2 + 3𝑥2 – 1)
then the polynomial is 2x2 + 3x – 2.
AP Board Textbook Solutions PDF for Class 10th Maths
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Ex 1.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 1 Real Numbers InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets Ex 2.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 2 Sets InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Ex 3.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 3 Polynomials InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Ex 4.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 5 Quadratic Equations InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Ex 6.5 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 6 Progressions InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 7 Coordinate Geometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Ex 8.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 8 Similar Triangles InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Ex 9.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Ex 10.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 10 Mensuration InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Ex 11.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 11 Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Ex 12.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 12 Applications of Trigonometry InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Ex 13.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability Optional Exercise Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 13 Probability InText Questions Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.1 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.2 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.3 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics Ex 14.4 Textbook Solutions PDF
- AP Board Class 10 Maths Chapter 14 Statistics InText Questions Textbook Solutions PDF






0 Comments:
Post a Comment