AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Book Answers ~ HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Thursday, June 9, 2022

AP Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions PDF: Download Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Book Answers

AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks Solutions and answers for students are now available in pdf format. Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Book answers and solutions are one of the most important study materials for any student. The Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 books are published by the Andhra Pradesh Board Publishers. These Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 textbooks are prepared by a group of expert faculty members. Students can download these AP Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 book solutions pdf online from this page.

Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks Solutions PDF

Andhra Pradesh State Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Books Solutions with Answers are prepared and published by the Andhra Pradesh Board Publishers. It is an autonomous organization to advise and assist qualitative improvements in school education. If you are in search of AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Books Answers Solutions, then you are in the right place. Here is a complete hub of Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 solutions that are available here for free PDF downloads to help students for their adequate preparation. You can find all the subjects of Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks. These Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks Solutions English PDF will be helpful for effective education, and a maximum number of questions in exams are chosen from Andhra Pradesh Board.

Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Books Solutions

Board	AP Board
Materials	Textbook Solutions/Guide
Format	DOC/PDF
Class	10th
Subject	Maths
Chapters	Maths Chapter 5 Quadratic Equations Ex 5.1
Provider	Hsslive

How to download Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions Answers PDF Online?

Visit our website - Hsslive
Click on the Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Answers.
Look for your Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks PDF.
Now download or read the Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions for PDF Free.

AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks Solutions with Answer PDF Download

Find below the list of all AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions for PDF’s for you to download and prepare for the upcoming exams:

10th Class Maths 5th Lesson Quadratic Equations Ex 5.1 Textbook Questions and Answers

Question 1.
Check whether the following are quadratic equations.
i) (x + l)² = 2(x-3)
Answer:
Given: (x + l)² = 2(x – 3)
⇒ x² + 2x + 1 = 2(x – 3) = 2x – 6
⇒ x² + 2x + l – 2x + 6 = 0
⇒ x² + 7 = 0 is a Q.E.

ii) x² – 2x = (-2) (3 – x)
Answer:
Given: x² – 2x = -2(3 – x)
⇒ x² – 2x = -6 + 2x
⇒ x² – 4x + 6 = 0 is a Q.E.

iii) (x-2) (x + 1) = (x- 1) (x + 3)
Answer:
Given: (x – 2) (x + 1) = (x – 1) (x + 3)
⇒ x (x + 1) – 2 (x +1)
= x (x + 3) – 1 (x + 3)
Note : Compare the coefficients of x2 on both sides. If they are equal it is not a Q.E.
⇒ x² + x – 2x – 2 = x² + 3x – x -3
⇒ x² – x – 2 = x² + 2x – 3
⇒ 3x – 1 = 0 is not a Q.E.

iv) (x – 3) (2x + 1) = x(x + 5)
Answer:
Given: (x – 3) (2x + 1) = x(x + 5)
⇒ x (2x + 1) – 3 (2x + 1) = x . x + 5 . x
⇒ 2x² + x – 6x – 3 = x² + 5x
⇒ 2x² – 5x – 3 – x² – 5x = 0
⇒ x² – 10x – 3 = 0 is a Q.E.
(or)
Comparing the coefficients of x2 on both sides.
x . 2x and x . x
⇒ 2x² and x²
2x² ≠ x²
Hence it’s a Q.E.

v) (2x – 1) (x – 3) = (x + 5) (x – 1)
Answer:
Given: (2x – 1) (x – 3) = (x + 5) (x – 1)
⇒ 2x (x – 3) -1 (x – 3) = x (x – 1) + 5(x – 1)
⇒ 2x² – 6x – x + 3 = x² – x + 5x – 5
⇒ 2x² -7x + 3 – x² – 4x + 5 = 0
⇒ x² – 11x + 8 = 0
Hence it’s a Q.E.
(or)
Co.eff. of x² on L.H.S. = 2 × 1 = 2
Co.eff. of x² on R.H.S = 1 × 1 = 1
LHS ≠ RHS Hence it is a Q.E.

vi) x² + 3x + 1 = (x – 2)²
Answer:
Given: x² + 3x + 1 = (x – 2)²
⇒ x² + 3x + 1 = x² – 4x + 4
⇒ 7x – 3 = 0 is not a Q.E.

vii) (x + 2)³ = 2x (x² – 1)
Answer:
Given: (x + 2)³ = 2x(x² – 1)
⇒ x³ + 6x² + 12x + 8 = 2x³ – 2x [∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
⇒ -x³ + 6x² + 14x + 8 = 0
is not a Q.E. [∵ degree = 3]

viii) x³ – 4x² – x + 1 = (x – 2)³
Answer:
Given : x³ – 4x² – x + 1 = (x – 2)³
⇒ x³ – 4x² – x + 1 = x³ – 6x² + 12x – 8
⇒ 6x² – 12x + 8 – 4x² – x + 1 = 0
⇒ 2x² – 13x + 9 = 0 is a Q.E.

Question 2.
Represent the following situations in the form of quadratic equations:
i) The area of a rectangular plot is 528 m². The length of the plot (in meters) is one more than twice its breadth. We need to find the length and breadth of the plot.
Answer:
Let the breadth of the rectangular plot be x m.
Then its length (by problem) = 2x + 1.
Area = l . b = (2x + 1) . x = 2x² + x
But area = 528 m² (∵ given)
∴ 2x² + x = 528
⇒ 2x² + x – 528 = 0 where x is the breadth of the rectangle.

ii) The product of two consecutive positive integers is 306. We need to find the integers.
Answer:
Let the consecutive integers be x and x + 1.
Their product = x(x + 1) = x² + x
By problem x² + x = 306
⇒ x² + x – 306 = 0
where x is the smaller integer.

iii) Rohan’s mother is 26 years older than him. The product of their ages after 3 years will be 360 years. We need to find Rohan’s present age.
Answer:
Let the present age of Rohan be x years.
Then age of Rohan’s mother = x + 26
After 3 years:
Age of Rohan would be = x + 3
Rohan’s mother’s age would be = (x + 26) + 3 = x + 29
By problem (x + 3) (x + 29) = 360
⇒ x(x + 29) + 3(x + 29) = 360
⇒ x² + 29x + 3x + 87 = 360
⇒ x² + 32x + 87 – 360 = 0
⇒ x² + 32x – 273 = 0
⇒ x² + 39x – 7x – 273 = 0
⇒ x (x + 39) – 7 (x + 39) = 0
⇒ (x – 7) (x + 39) = 0
⇒ x = 7 or x = -39 ‘x’ being age cannot be negative.
∴ x = Present age of Rohan = 7 years.

iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Answer:
Let the speed of the train be x km/h.
Then time taken to travel a distance of distance of 480 km = distance speed = 480𝑥
If the speed is 8km/h less, then time needed to cover the same distance would be 480𝑥−8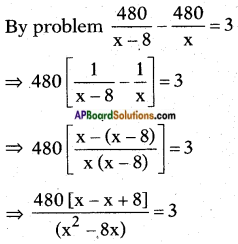

⇒ x² – 8x = 1280
⇒ x² – 8x – 1280 = 0
where x is the speed of the train.

AP Board Textbook Solutions PDF for Class 10th Maths

AP Board Class 10 Maths Chapter 1 Real Numbers Textbook Solutions PDF

AP Board Class 10 Maths Chapter 2 Sets Textbook Solutions PDF

AP Board Class 10 Maths Chapter 3 Polynomials Textbook Solutions PDF

AP Board Class 10 Maths Chapter 4 Pair of Linear Equations in Two Variables Textbook Solutions PDF

AP Board Class 10 Maths Chapter 5 Quadratic Equations Textbook Solutions PDF

AP Board Class 10 Maths Chapter 6 Progressions Textbook Solutions PDF

AP Board Class 10 Maths Chapter 7 Coordinate Geometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 8 Similar Triangles Textbook Solutions PDF

AP Board Class 10 Maths Chapter 9 Tangents and Secants to a Circle Textbook Solutions PDF

AP Board Class 10 Maths Chapter 10 Mensuration Textbook Solutions PDF

AP Board Class 10 Maths Chapter 11 Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 12 Applications of Trigonometry Textbook Solutions PDF

AP Board Class 10 Maths Chapter 13 Probability Textbook Solutions PDF

AP Board Class 10 Maths Chapter 14 Statistics Textbook Solutions PDF

Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks for Exam Preparations

Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions can be of great help in your Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 exam preparation. The AP Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks study material, used with the English medium textbooks, can help you complete the entire Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Books State Board syllabus with maximum efficiency.

FAQs Regarding Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Solutions

How to get AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook Answers??

Students can download the Andhra Pradesh Board Class 10 Maths Chapter 5 Quadratic Equations Ex 5.1 Answers PDF from the links provided above.

Can we get a Andhra Pradesh State Board Book PDF for all Classes?

Yes you can get Andhra Pradesh Board Text Book PDF for all classes using the links provided in the above article.

Important Terms

Andhra Pradesh Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1, AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks, Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1, Andhra Pradesh State Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook solutions, AP Board Class 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks Solutions, Andhra Pradesh Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1, AP Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks, Andhra Pradesh State Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1, Andhra Pradesh State Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbook solutions, AP Board STD 10th Maths Chapter 5 Quadratic Equations Ex 5.1 Textbooks Solutions,

HSSlive: Plus One & Plus Two Notes & Solutions for Kerala State Board

Hsslive.co.in: Kerala Higher Secondary News, Plus Two Notes, Plus One Notes, Plus two study material, Higher Secondary Question Paper.

Thursday, June 9, 2022